Виды деформаций деталей: растяжение, сжатие, сдвиг, кручение, изгиб

Расчет на прочность: при растяжении, кручении и изгибе.

Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).

Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.

В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь. Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.

Деформации на примере организма человека

Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:

• Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
• Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
• Изгиб характерен для конечностей, костей таза, позвонков.
• Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.

Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.

По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.

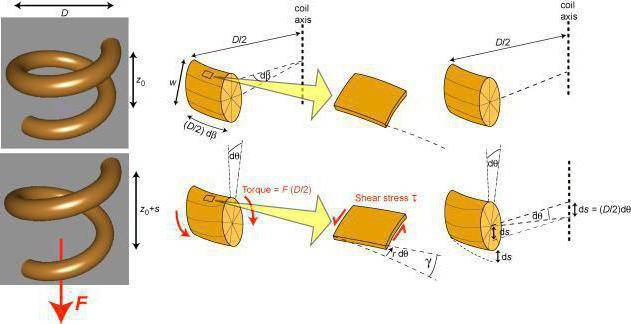
Деформация сжатия

Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5

а — для пластических материалов; б — для хрупких материалов ; в — для дерева вдоль волокон, г — для дерева поперек волокон.

Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 — 318.5.

Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.

Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.

Расчеты на прочность при растяжении (сжатии)

Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.

Физическая природа деформации металлов

Этот процесс включает в себя упругую и остаточную стадии. Возникающие при этом деформации подразделяются на три группы:

1. Упругие, т.е., такие, которые полностью исчезают при снятии приложенных внешних сил. Тело при этом приобретает свои первоначальные размеры. Изучением упругих деформаций занимаются теория упругости и сопротивление материалов. Связь между напряжениями и деформациями в этом случае линейна и подчиняется закону Гука.

2. Упругопластические, которые возникают тогда, когда упругая и пластическая (остаточная) составляющие соизмеримы между собой. Изучение упругопластических деформаций имеет значение для всесторонней оценки запаса прочности металла, поскольку в практике металлообработки такой вид деформации не используется.

3. Пластические/конечные, при которых упругие изменения формы незначительны, и ими можно пренебречь. Здесь зависимость напряжений и деформаций не носит линейного характера, и зависит от множества факторов.

Любой реальный металл представляет собой совокупность анизотропных кристаллов, ориентация которых произвольна. Поэтому предполагается, что во всех направлениях имеется приблизительно одинаковое количество одинаково ориентированных зёрен. Именно поэтому свойства металла во всех направлениях одинаковы и определяются некоторыми средними значениями. Квазиизотропность металлов облегчает изучение физических основ их деформирования.

Основой для любого изменения формы металла является наличие дефектов в его структуре, прежде всего – дислокаций. С помощью теории дислокаций объясняются механизмы разрушения металла, его кристаллизация, упрочнение/разупрочнение и пр. Ключевым положением теории дислокации является то, что любое изменение формы представляет собой результат перемещения и размножения дефектов в кристаллической решётке. При этом механизм деформации рассматривается на уровне отдельных атомов. Такое представление позволяет анализировать многие физические явления, происходящие в деформируемом теле под нагрузками, при повышенных температурах и т.д.

Пластичность и хрупкость

Тело из любого материала при малых деформациях ведет себя как упругое. В то же время почти все тела в той или иной мере могут испытывать пластические деформации. Существуют хрупкие тела.

Механические свойства материалов разнообразны. Такие материалы, как резина или сталь, обнаруживают упругие свойства до сравнительно больших напряжений и деформаций. Для стали, например, закон Гука выполняется вплоть до ε = 1%, а для резины – до значительно больших ε, порядка десятков процентов. Поэтому такие материалы называют упругими.

У мокрой глины, пластилина или свинца область упругих деформаций мала. Материалы, у которых незначительные нагрузки вызывают пластические деформации, называют пластичными.

Деление материалов на упругие и пластичные в значительной мере условно. В зависимости от возникающих напряжений один и тот же материал будет вести себя или как упругий, или как пластичный. Так, при очень больших напряжениях сталь обнаруживает пластичные свойства. Это широко используют при штамповке стальных изделий с помощью прессов, создающих огромную нагрузку.

Холодная сталь или железо с трудом поддаются ковке молотом. Но после сильного нагрева им легко придать посредством ковки любую форму. Пластичный при комнатной температуре свинец приобретает ярко выраженные упругие свойства, если его охладить до температуры ниже –100 °С.

Большое значение на практике имеет свойство твердых тел, называемое хрупкостью. Тело называют хрупким, если оно разрушается при небольших деформациях. Изделия из стекла и фарфора хрупкие: они разбиваются на куски при падении на пол даже с небольшой высоты. Чугун, мрамор, янтарь также обладают повышенной хрупкостью. Наоборот, сталь, медь, свинец не являются хрупкими.

Отличительные особенности хрупких тел легче всего уяснить с помощью зависимости σ от ε при растяжении. На рисунке 11, а, б изображены диаграммы растяжений чугуна и стали. На них видно, что при растяжении чугуна всего лишь на 0,1% в нем возникает напряжение около 80 МПа, тогда как в стали оно при такой же деформации равно лишь 20 МПа.

Рис. 11

Чугун разрушается сразу при удлинении на 0,45%, почти не испытывая предварительно пластических деформаций. Предел прочности его равен 1,2∙108 Па. У стали же при ε = 0,45% деформация все еще остается упругой и разрушение происходит при ε ≈ 15%. Предел прочности стали равен 700 МПа.

У всех хрупких материалов напряжение очень быстро растет с удлинением, и они разрушаются при весьма малых деформациях. Пластичные свойства у хрупких материй лов практически не проявляются.

Пластическая деформация

Теория дислокаций утверждает, что с приложением нагрузки к реальным кристаллам металла смещение одной части кристалла относительно другой происходит не одновременно по всей площади скольжения. Начинается оно в точке дефекта кристалла и распространяется при значительно меньшем внешнем усилии, чем при одновременном скольжении целого блока атомов. Значительное расхождение между теоретическими и фактическими значениями напряжений (например, для меди оно составляет 1540 МПа и 1 МПа, для железа – 2300 МПа и 29 МПа) объясняется наличием в стали структурных дефектов, около которых сдвиг вначале локализуется, а затем распространяется вместе с самим дефектом с некоторой скоростью.

Дислокации располагаются в наиболее плотноупакованных плоскостях кристаллической решётки. При возрастании нагрузки первыми начинают двигаться дислокации той плоскости скольжения, в которых касательные напряжения максимальны. Для начала пластического течения необходимо, чтобы касательное напряжение превышало критическое значение, величина которого зависит от исходной структуры деформируемого металла. Данное обстоятельство предопределяет необходимость учёта истории деформирования материала, что позволяет определять количественные и качественные параметры процесса пластической деформации.

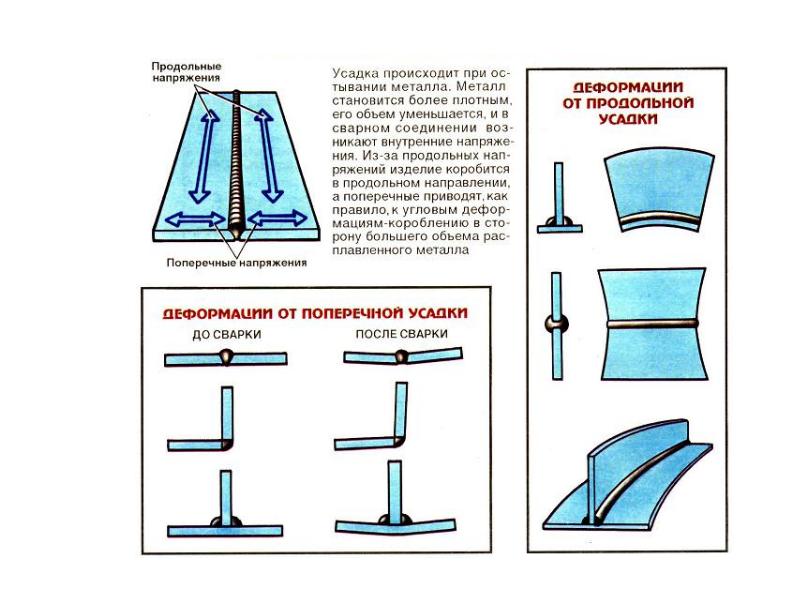
Виды пластической деформации металлов определяются характером перемещения кристаллов во время приложения усилия. Такое перемещение может происходить скольжением и двойникованием.

Скольжение

Скольжение является основным видом пластической деформации идеального кристалла. Обычно в качестве плоскостей скольжения выступают плоскости с наибольшей плотностью расположения атомов, а направлениями скольжения являются направления, по которым межатомные расстояния имеют минимальное значение.

В гексагональной решётке можно провести только одну плоскость, в которой расположено наибольшее число атомов – это плоскость основания. В решётках кубической формы таких плоскостей больше. Поэтому при прочих равных условиях металлы с гексагональной решёткой менее пластичны, чем металлы с кубической решёткой.

Пластическое деформирование начинается, прежде всего, в тех плоскостях скольжения, и по тем направлениям, которые расположены под оптимальным углом по отношению к внешней силе. Так, при сжатии и растяжении пластическая деформация возникает в первую очередь в плоскостях, расположенных под углом 45
к линии действия внешней силы.

Скольжение является сдвиговым деформационным процессом. Известно, что если отполированный образец из моно- или поликристалла подвергнуть нагружению, то при определённой нагрузке на поверхности образца появляются сетки линий скольжения, называемые линиями Чернова-Людерса. Эти линии качественно характеризуют сдвиг одних частей образца относительно других.

Двойникование

В некоторых металлах – магнии, цинке, золоте, железе – наряду со скольжением наблюдается двойникование. При двойниковании происходит поворот деформированной части кристалла в положение, зеркальное по отношению к деформированному. Однако и в этом случае происходит сдвиг атомов в новые положения устойчивого равновесия на расстояния, которые пропорциональны основному параметру решётки.

Двойникование часто возникает при ударном деформировании и распространено для металлов и сплавов, кристаллизация которых происходила с образованием кристаллитов в форме многогранников.

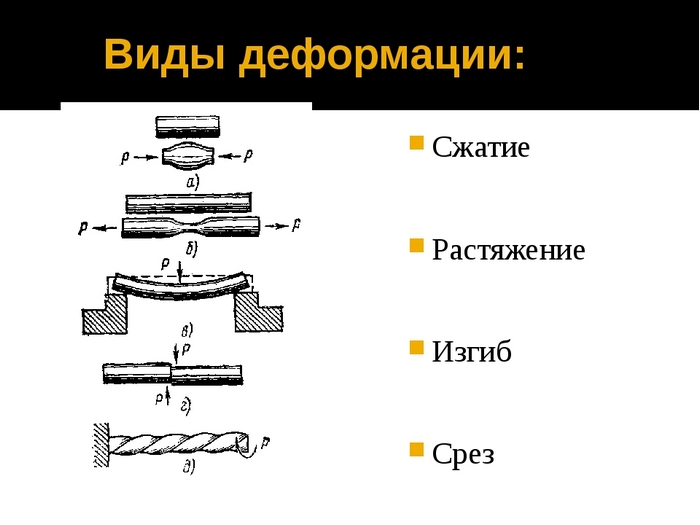
Влияние температуры на изменение механических свойств материалов

Твердое состояние — не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.

Таблица 318.6. Температуры плавления некоторых веществ

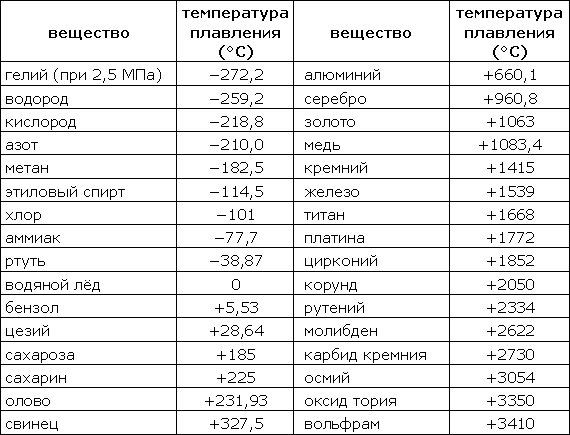
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).

Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.

При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.

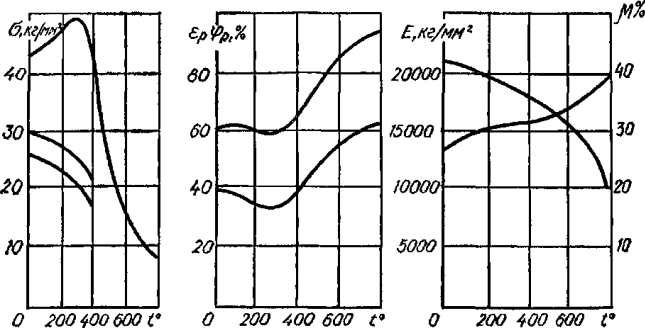
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.

При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.

Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия — увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.

ИЗГИБ

ИЗГИБ

– один из основных видов деформации балки, когда прямолинейная балка под действием внешних нагрузок приобретает криволинейную форму. (Корни слова «балка» – немецкие и первоначально это слово означало «бревно»). Во многих конструкциях балка является основным элементом; примером являются многие типы перекрытий, мостов и т.д. Также по теме: МЕХАНИКА

Балка как конструктивный элемент обычно или закреплена концами на соответствующих опорах, или одним концом заделана в стену, тогда как другой конец оказывается свободным (в этом случае балку называют «консоль»), рис.1 (а, б).

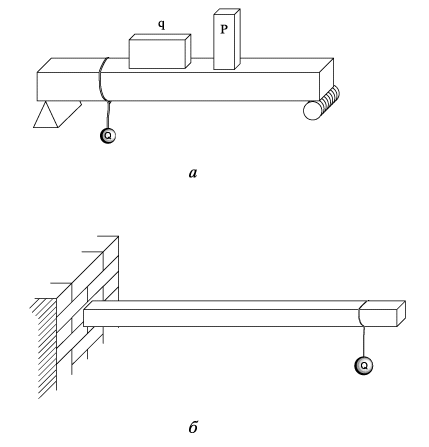
В некоторых местах балка взаимодействуют с другими телами; схематизируя ситуацию (рис. 2), говорят, что в известных точках к балке приложены заданные сосредоточенные силы P

,Q или распределенные нагрузки интенсивностиq (килоньютонов на метр).

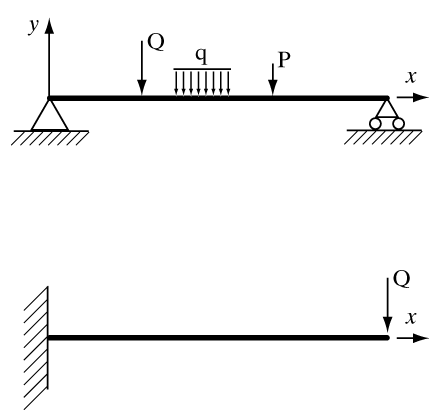
Примером распределенных нагрузок является собственный вес балки или вес достаточно длинного постороннего тела, лежащего на балке (например, снега). Нагрузки (или их часть), направленные перпендикулярно к балке, вызывают ее изгиб; направленные вдоль балки вызывают растяжение или сжатие. Задачей теории изгиба балок является определение прогиба балки под нагрузками, а также напряжений и деформаций в материале балки, естественно, что форма, размеры, материал балки и внешние нагрузки считаются заданными. Затем, при расчете на прочность, задачу трансформируют так: каковы должны быть размеры сечения балки, чтобы при заданных нагрузках напряжения не превышали бы допустимых значений?

Теория изгиба балки была создана Я.Бернулли и Л.Эйлером на рубеже 17–18 вв. Для простоты балка заменяется отрезком прямой, причем считается, что упругие свойства этого отрезка такие же, как у исходной балки. После приложения нагрузок отрезок изгибается и становится криволинейным. Получившаяся кривая называется упругой линией или эластикой. Задача – найти ее уравнение у

=f (x ). Решение этой задачи основано на утверждении, что в каждой точке упругой линии ее кривизна пропорциональна изгибающему моменту внешних сил, который зависит от координатыx и обозначаетсяM (x ). Так как при малых прогибах, которые в первую очередь интересуют инженеров, кривизна кривой практически равна ее второй производной, можно записать дифференциальное уравнение:

Коэффициент пропорциональности EJ

называется изгибной жесткостью, он определяет способность балки сопротивляться изгибу и равен произведению модуля упругости материала балкиE на момент инерции сечения балкиJ , который для прямоугольного бруса выражается формулой

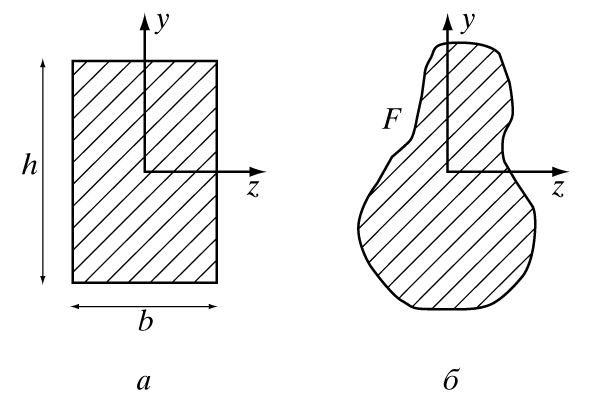
где b

– ширина сечения, аh – высота (рис. 3,а).

Если сечение балки есть фигура F

(рис. 3,б), и начало координат проходит через центр масс сечения, то

J

= тт y\up122dF т.е. момент инерции площади F

определяется как двойной интеграл по этой площади. Название «момент инерции» связано с тем, что этот интеграл в динамике твердого тела связан с инерционными характеристиками тела.

Изгибная жесткость учитывает и упругость материала, и форму и размеры сечения балки.

Изгибающий момент M

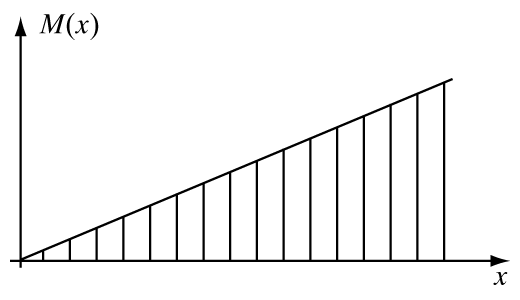
(x ) полностью определяется величиной и положением нагрузок и находится по правилам статики. Например, если в консольной балке, нагружаемой на конце силойP , (рис. 2), мысленно провести сечение через точку с координатойx , то момент силыP относительно точкиx выражается очевидной формулой

M = Px

(система координат показана на рис. 4), при изменении расстояния сечения от конца балки момент M

растет линейно; этот график называют эпюрой изгибающего моментаM (x ). Напряжения s в сечениях балки пропорциональныM (x ):

(координата y

отсчитывается вверх от центра сечения).

В качестве примера можно рассмотреть две одинаковые балки: одну – на двух шарнирных опорах, другую – консольную, нагруженные одинаковыми силами P

в середине пролета и на конце соответственно. Длина балокl , сечение – прямоугольникb ×h . Прогиб первой балки в середине пролета равен

Прогиб на конце второй балки равен

Для сравнения укажем, что если ту же балку растягивать силой P

, то ее удлинение будет равно . Напряжения и деформации в изогнутой балке распределены таким образом, что внешние волокна растянуты, а внутренние – сжаты, причем и напряжения s, и деформации e растут пропорционально расстоянию от середины сечения балки, точнее – от нейтральной линии, где s = 0, и e = 0. Другими словами, внешние слои балки несут большую часть нагрузки, внутренние – значительно меньшую. Поэтому целесообразно так организовать форму сечения балки, чтобы большая часть материала была удалена от центра сечения. Двутавровые (т.е. в виде двойного «Т») и трубчатые сечения балок являются типичными примерами оптимальных (т.е. наилучших в некотором смысле) сечений.

Предел прочности

Определение 9

Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.

В точке e материал разрушается.

Определение 10

Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.

Определение 11

Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.

Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:

∆xl=1GFS

Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Нм2, G=,42·1011 Нм2.

Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен. При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела

При малых деформациях

Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

∆VV=1Bp

Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Нм2, у стали B=1,6·1011Нм2. В Тихом океане на глубине 4 км давление составляет 4·107 Нм2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно ,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.

От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.

Всё ещё сложно? Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Деформация металла. Упругая и пластическая деформация

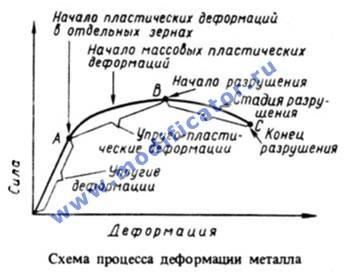
Влияние упругой (обратимой) деформации на форму, структуру и свойства тела полностью устраняется после прекращения действия вызвавших её сил (нагрузок), так как под действием приложенных сил происходит только незначительное смещение атомов или поворот блоков кристалла. Сопротивление металла деформации и разрушению называется прочностью. Прочность является первым требованием, предъявляемым к большинству изделий.

Модуль упругости – это характеристика сопротивления материалов упругой деформации. При достижении напряжениями так называемого предела упругости (или порога упругости) деформация становится необратимой.

Пластическая деформация, остающаяся после снятия нагрузки, связана с перемещением атомов внутри кристаллов на относительно большие расстояния и вызывает остаточные изменения формы, структуры и свойств без макроскопических нарушений сплошности металла. Пластическую деформацию также называют остаточной или необратимой. Пластическая деформация в кристаллах может осуществляться скольжением и двойникованием.

Пластическая деформация металла. Для металлов характерно большее сопротивление растяжению или сжатию, чем сдвигу. Поэтому процесс пластической деформации металла обычно представляет собой процесс скольжения одной части кристалла относительно другой по кристаллографической плоскости или плоскостям скольжения с более плотной упаковкой атомов, где наименьшее сопротивление сдвигу. Скольжение осуществляется в результате перемещения в кристалле дислокаций. В результате скольжения кристаллическое строение перемещающихся частей не меняется.

Другим механизмом пластической деформации металла является двойникование. При деформации двойникованием напряжение сдвига выше, чем при скольжении. Двойники обычно возникают тогда, когда скольжение по тем или иным причинам затруднено. Деформация двойникованием обычно наблюдается при низких температурах и высоких скоростях приложения нагрузки.

Пластичность – это свойство твёрдых тел под действием внешних сил изменять, не разрушаясь, свою форму и размеры и сохранять остаточные (пластические) деформации после устранения этих сил. Отсутствие или малое значение пластичности называется хрупкостью. Пластичность металлов широко используется в технике.