Конусность и уклон: построение, расчет, обозначение

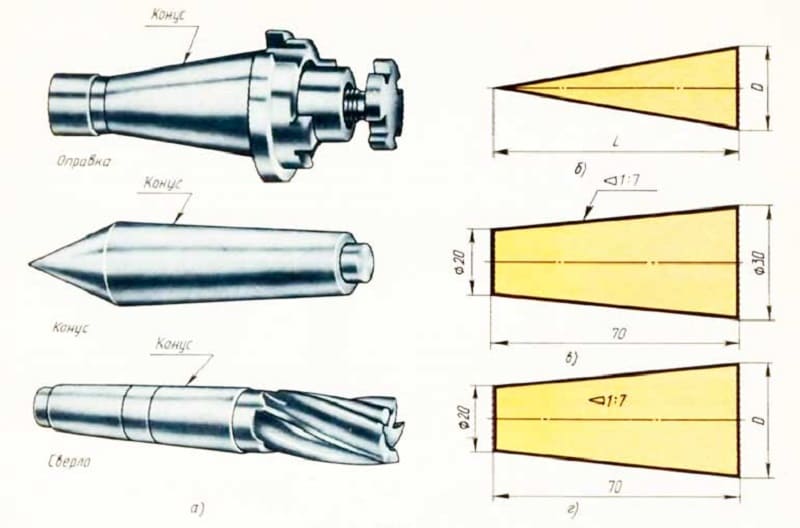
Уклоны и конусность — Техническое черчение

• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

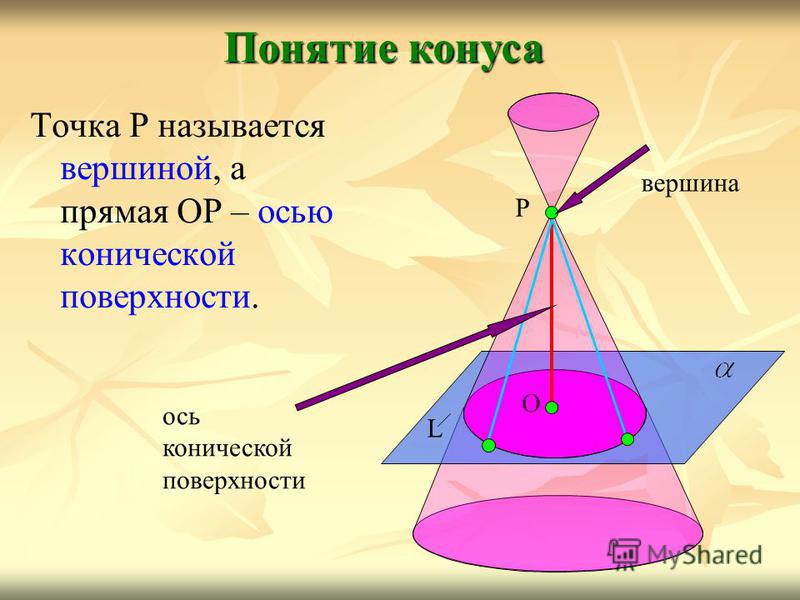
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

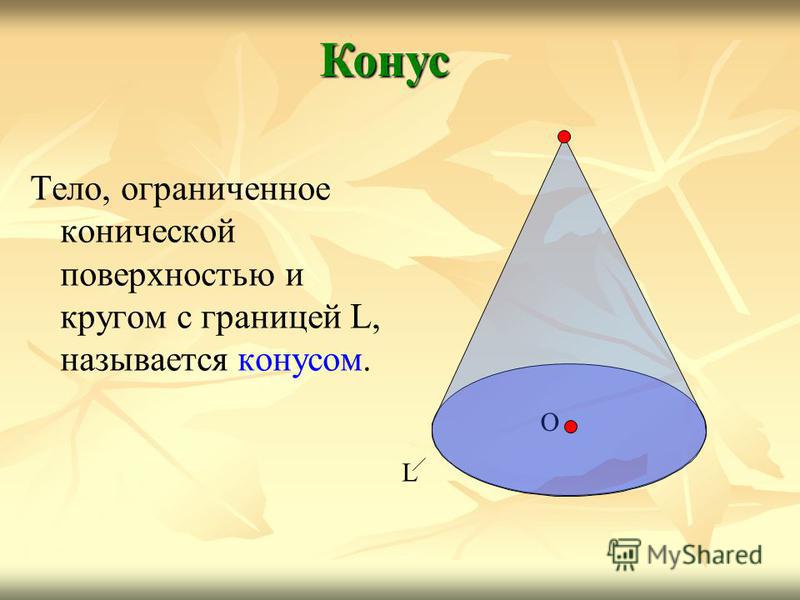
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

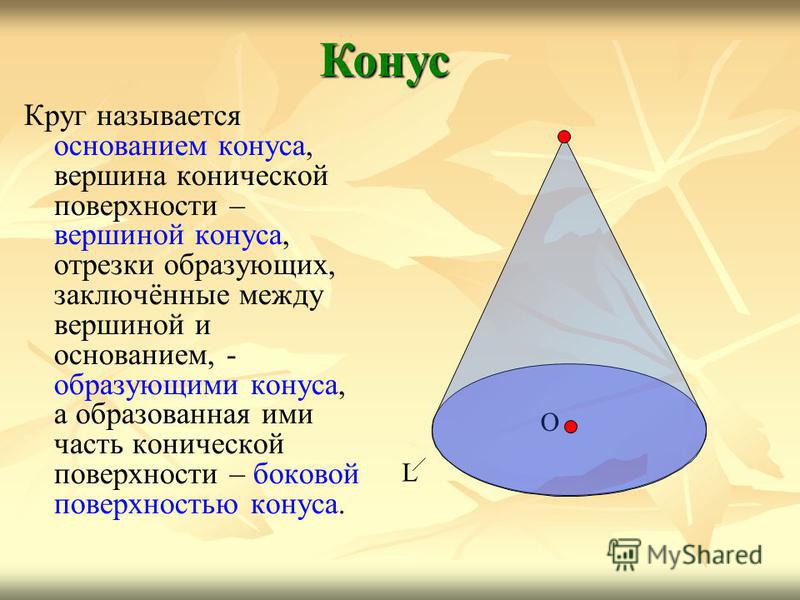
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

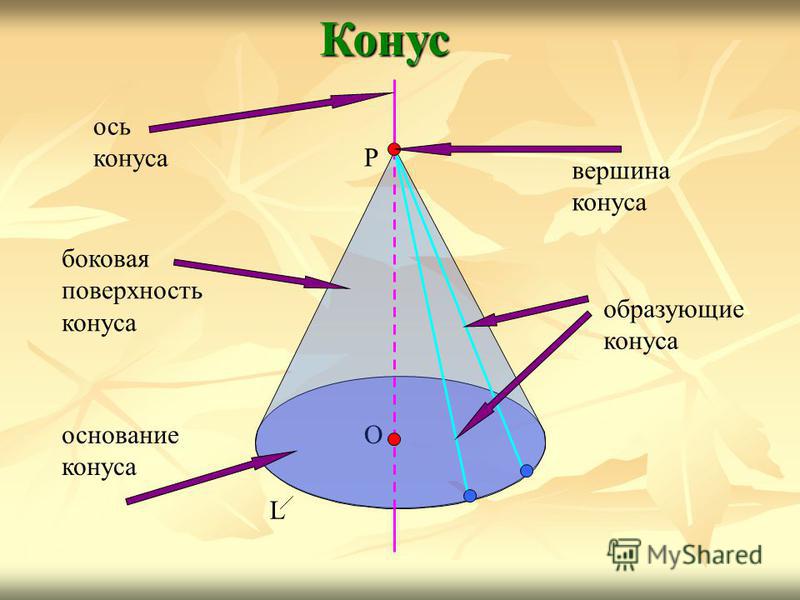
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

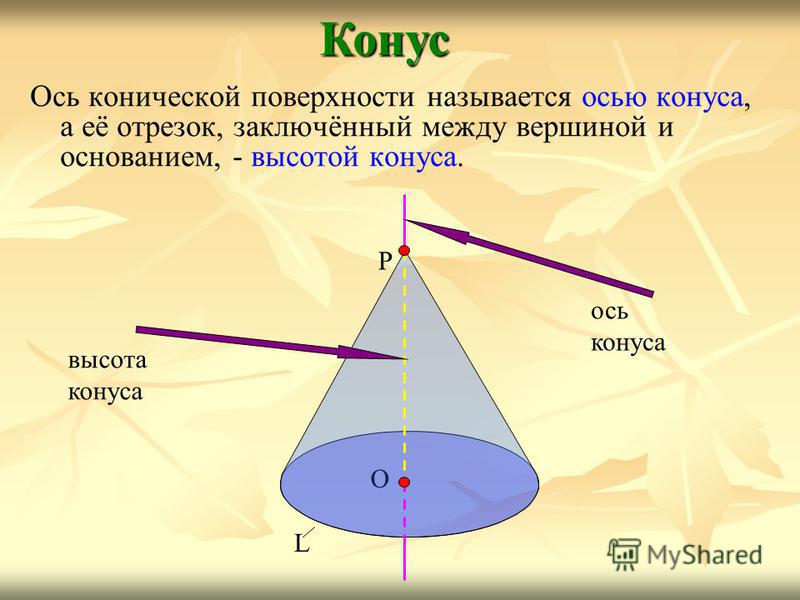
8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

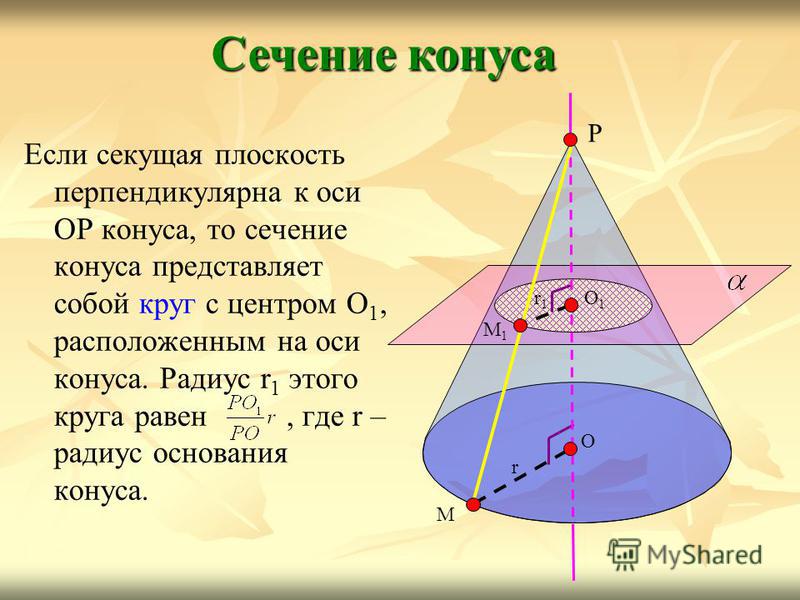
11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

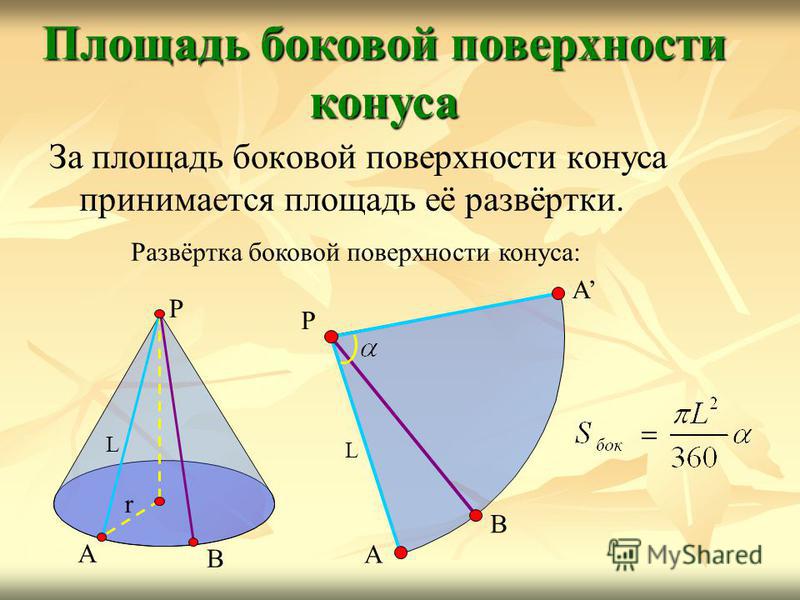
13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

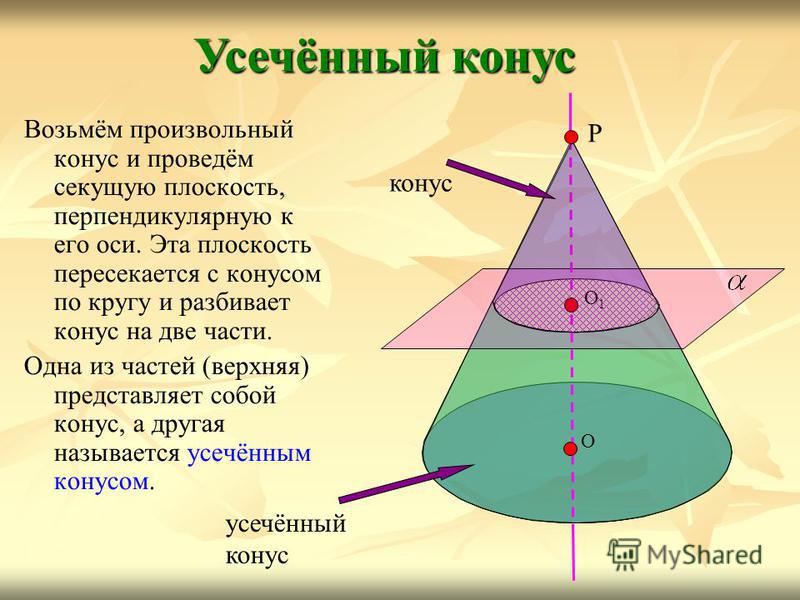
16

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

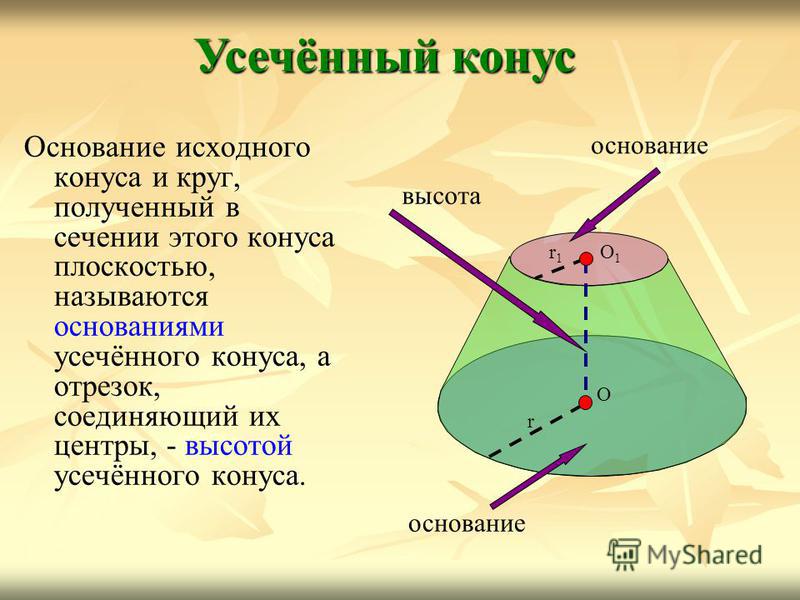
17

Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

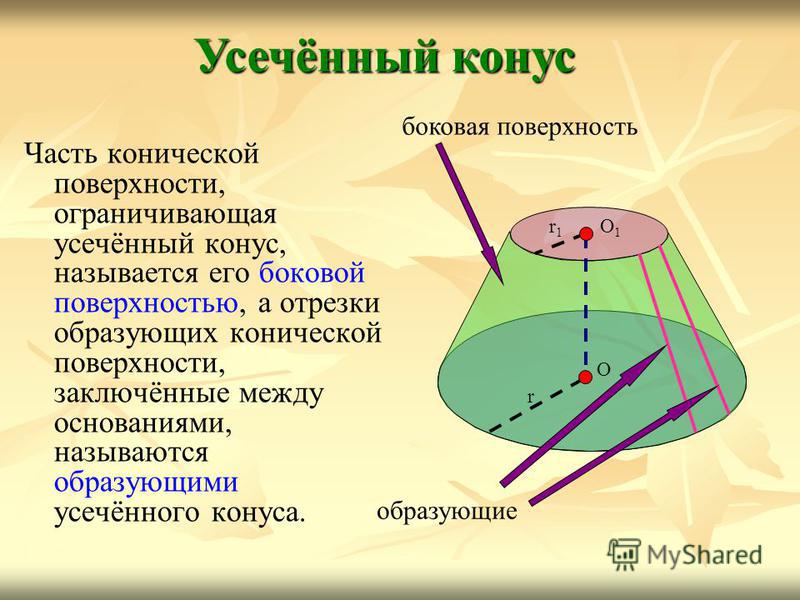
18

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

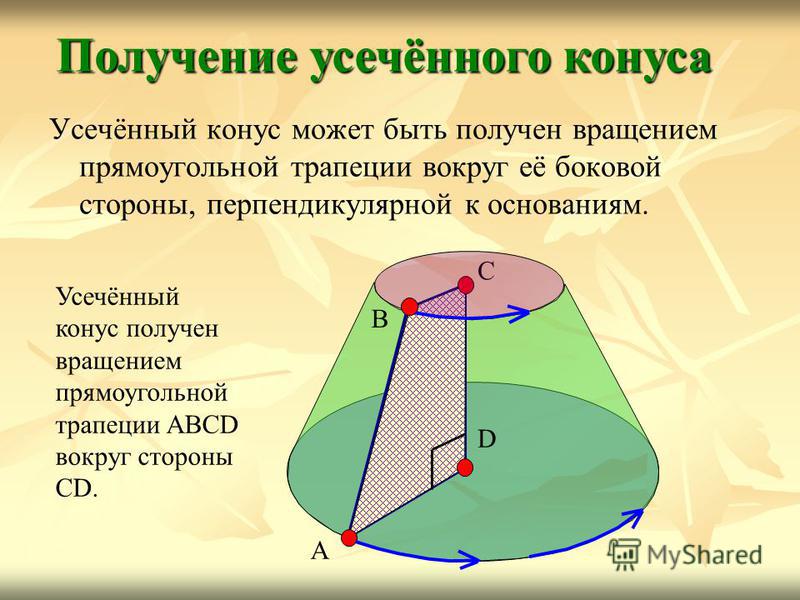
19

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

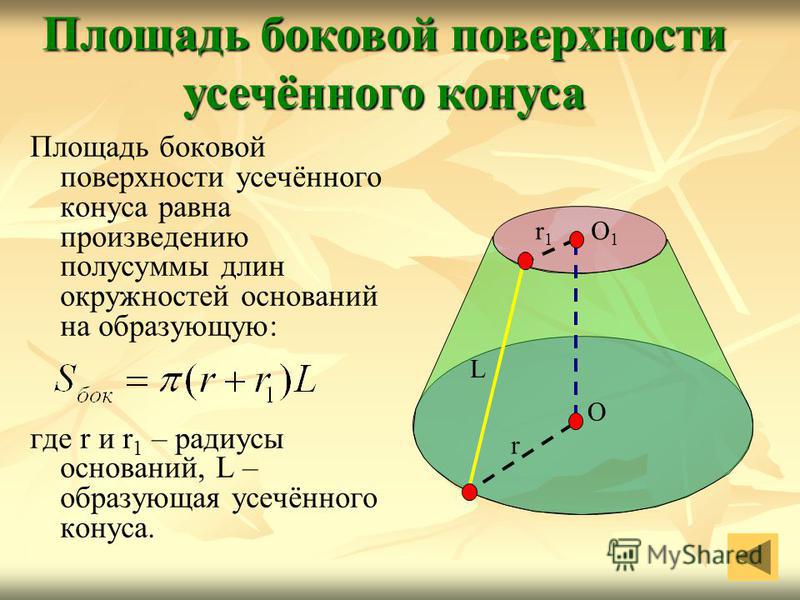
Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:

1. Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
2. Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
3. Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
4. Есть возможность провести замер всех показателей при применении соответствующих инструментов.
5. Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.

R Калибры для трубной конической резьбы (1/16″ — 6″) ГОСТ 7157-79

Назначение:

Тип резьбы: треугольная коническая Угол профиля: 55° Конусность: 1:16Цена: по запросу Оставить заявку

Примеры обозначения при заказе: Пробка R 1.1/2″ Р-P ГОСТ 7157-79 Кольцо R 1.1/2″ Р-P ГОСТ 7157-79 исп.2 Пробка R 1.1/2″ К-P ГОСТ 7157-79 (исполнение 1 в заказе не указывается)

Типы конусных калибров
рабочие пробки и кольца (2 исполнения)
Р-Р	резьбовые
Р-СП	резьбовые специальные
Р-Г	гладкие
контрольные пробки и кольца (контркалибры)
К-Р	резьбовые для колец типа Р-Р
К-СП	резьбовые для колец типа Р-СП
К-Г	гладкие для колец типа Р-Г

Примечания:

• Рабочие пробки и кольца (типы Р-Р, Р-Г и Р-СП) изготавливаются в следующих исполнениях: с измерительной плоскостью, соответствующей номинальному положению основной плоскости резьбы;
• с измерительными плоскостями, соответствующими номинальному положению основной плоскости, а также наибольшему и наименьшему предельным размерам осевого смещения основной плоскости резьбы.

Контрольные пробки (типы К-Р, К-Г и К-СП) изготавливаются только в исполнении 1.
Исполнение 2 является предпочтительным.

Таблица типоразмеров (номинальных диаметров и шагов резьбы)
1/16″ х 0,907	1″ х 2,309	3 1/2″ х 2,309
1/8″ х 0,907	1 1/4″ х 2,309	4″ х 2,309
1/4″ х 1,337	1 1/2″ х 2,309	5″ х 2,309
3/8″ х 1,337	2″ х 2,309	6″ х 2,309
1/2″ х 1,814	2 1/2″ х 2,309
3/4″ х 1,814	3″ х 2,309

Ассортимент производимой продукции:

Пробка R 1/8″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1/8″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 1/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 3/8″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 3/8″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 3/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 3/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 1″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 1.1/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1.1/4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 1.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 1.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 2.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 2.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 3″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 3″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 3.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 3.1/2″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 4″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 5″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 5″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Пробка R 6″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81 Кольцо R 6″ Р-P (Р-СП, Р-Г, К-Р, К-СП, К-Г) ГОСТ 6211-81

По вопросам покупки калибров обращайтесь в отдел продаж по телефону +7 (351) 734-96-34 и на электронную почту

Перевод конусности в градусы

Конусность – отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.

Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10. Отмечаем точки BC и строим треугольник DKP так, чтобы KP:BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:

здесь угол φ представлен в радианах.

где L – расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана конусность например 1 : 2,5 откуда i=1:5 и tgφ=0,2 тогда перевод ее в градусы выполняется по формулам:

Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов

Обозна- чение	конуса	Конус-	ность	Угол	конуса	Угол	уклона
Ряд 1	Ряд 2	Угл. ед.	Рад.	Угл. ед.	Рад.
1:500	1:500	0,0020000	6`52,5″	0,0020000	3`26,25″	0,0010000
1:200	1:200	0,0050000	17`11,3″	0,0050000	8`25,65″	0,0025000
1:100	1:100	0,0100000	34`22,6″	0,0100000	17`11,3″	0,0050000
1:50	1:50	0,0200000	1°8`45,2″	0,0199996	34`22,6″	0,0099998
1:30	1:30	0,0333333	1°54`34,9″	0,0333304	57`17,45″	0,0166652
1:20	1:20	0,0500000	2°51`51,1″	0,0499896	1°25`55,55″	0,0249948
1:15	1:15	0,0666667	3°49`5,9″	0,0666420	1°54`32,95″	0,0333210
1:12	1:12	0,0833333	4°46`18,8″	0,0832852	2°23`9,4″	0,0416426
1:10	1:10	0,1000000	5°43`29,3″	0,0999168	2°51`44,65″	0,0499584
1:8	1:8	0,1250000	7°9`9,6″	0,1248376	3°34`34,8″	0,0624188
1:7	1:7	0,1428571	8°10`16,4″	0,1426148	4°5`8,2″	0,0713074
1:6	1:6	0,1666667	9°31`38,2″	0,1662824	4°45`49,1″	0,0831412
1:5	1:5	0,2000000	11°25`16,3″	0,1993374	5°42`38,15″	0,0996687
1:4	1:4	0,2500000	14°15`0,1″	0,2487100	7°7`30,05″	0,1243550
1:3	1:3	0,3333333	18°55`28,7″	0,3302972	9°27`44,35″	0,1651486
30°	1:1,866025	0,5358985	30°	0,5235988	15°	0,2617994
45°	1:1,207107	0,8284269	45°	0,7853982	22°30`	0,3926991
60°	1:0,866025	1,1547010	60°	1,0471976	30°	0,5235988
75°	1:0,651613	1,5346532	75°	1,3089970	37°30`	0,6544985
90°	1:0,500000	2,0000000	90°	1,5707964	45°	0,7853982
120°	1:0,288675	3,4641032	120°	2,0943952	60°	1,0471976

Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

Конусность поверхности

обозначается на чертеже: – надписью Конусность с указанием ее величины; – указывающей на нее стрелкой с полкой где пишется: – Конусность с указанием ее величины; – знак конусности и ее величина.

Калькулятор и формула для вычисления конусности детали.

Конусность может быть определена как отношение разности наибольшего диаметра конуса и наименьшего диаметра конуса к длине конуса, тогда формула для определения конусности детали будет иметь нижеследующий вид:

Также конусность детали можно вычислить как двойной тангенс угла наклона конуса, такая формула будет следующей:

Для определения конусности необходимо ввести значения наибольшего диаметра конуса, наименьшего диаметра конуса, длины конуса и нажать кнопку «ВЫЧИСЛИТЬ.»

Результатом вычисления будет значение конусности детали.

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

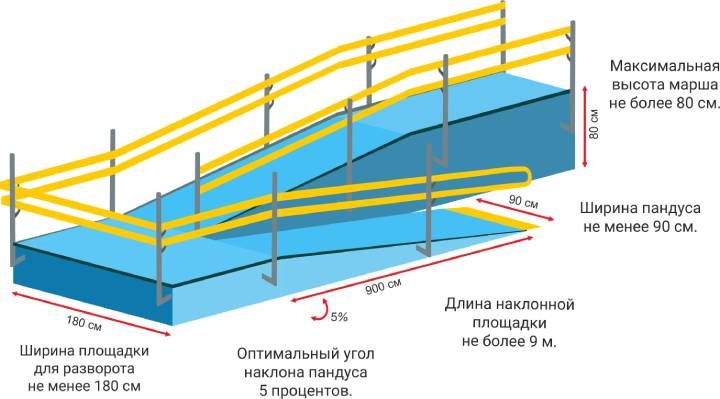
Нормативы для пандусов 2021

По нормативам СП 59.13330.2016 (с учетом вступивших в силу изменений 15 Мая 2021 года) пандус должен иметь следующие характеристики:

Список документации, рекомендуемой к ознакомлению:

1. СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
2. ГОСТ Р 51261-2017 содержит технические требования к стационарным опорным устройствам.
3. СП 30-102-99 содержит требования к входной площадке.
4. СП 59.13330.2016 содержит предписания по доступности зданий и сооружений для маломобильных групп населения

Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем /спуск получается в разы выше. Угол наклона — это соотношение длины к высоте подъема.

Запомните! При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.

Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:

• При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
• Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
• Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
• Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
• Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
• Поверхность пандуса должна быть нескользкой текстурой.
• Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

Конус Морзе и метрический конус

Конус Морзе — одно из самых широко применяемых креплений инструмента. Был предложен Стивеном А. Морзе приблизительно в 1864 году .

Конус Морзе подразделяется на восемь размеров, от КМ0

доКМ7 (англ. MT0-MT7 , нем. MK0-MK7 ) . Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26″ до 3°00’52″, уклон конуса от 1°25’43″ до 1°30’26″) в зависимости от типоразмера.

Метрический конус

По мере развития станкостроения понадобилось расширить диапазон размеров конусов Морзе как в большую, так и в меньшую стороны. При этом, для новых типоразмеров конуса, выбрали конусность ровно 1:20 (угол конуса 2°51’51″, уклон конуса 1°25’56″) и назвали их метрическими конусами

(англ. Metric Taper ). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2006 также определяет уменьшенные метрические конуса № 4 и № 6 (англ. ME4, ME6 ) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80 — ME200 ).

Конструктивных различий между конусом Морзе и метрическим нет.

Размеры наружного и внутреннего конуса (по ГОСТ 25557-2006), мм

Таблица 1

Обозначение конуса	Конусность	D	D 1	d	d 1	d 2	d 3 max	d 4 max	d 5	l 1 max	l 2 max	l 3 max	l 4 max	l 5 min	l 6
Метрический	№ 4	1:20	4	4,1	2,9	—	—	—	2,5	3	23	25	—	—	25	21
№ 6	1:20	6	6,2	4,4	—	—	—	4	4,6	32	35	—	—	34	29
Морзе	КМ0	1:19,212	9,045	9,2	6,4	—	6,1	6	6	6,7	50	53	56,3	59,5	52	49
КМ1	1:20,047	12,065	12,2	9,4	M6	9	8,7	9	9,7	53,5	57	62	65,5	56	52
КМ2	1:20,020	17,780	18	14,6	M10	14	13,5	14	14,9	64	69	75	80	67	62
КМ3	1:19,922	23,825	24,1	19,8	M12	19,1	18,5	19	20,2	80,1	86	94	99	84	78
КМ4	1:19,254	31,267	31,6	25,9	M16	25,2	25,2	24	26,5	102,5	109	117,5	124	107	98
КМ5	1:19,002	44,399	44,7	37,6	M20	36,5	35,7	35,7	38,2	129,5	136	149,5	156	135	125
КМ6	1:19,180	63,348	63,8	53,9	M24	52,4	51	51	54,6	182	190	210	218	188	177
КМ7	1:19,231	83,058	—	285.75	294.1
Метрический	№ 80	1:20	80	80,4	70,2	M30	69	67	67	71,5	196	204	220	228	202	186
№ 100	1:20	100	100,5	88,4	M36	87	85	85	90	232	242	260	270	240	220
№ 120	1:20	120	120,6	106,6	M36	105	102	102	108,5	268	280	300	312	276	254
№ 160	1:20	160	160,8	143	M48	141	138	138	145,5	340	356	380	396	350	321
№ 200	1:20	200	201	179,4	M48	177	174	174	182,5	412	432	460	480	424	388

Укороченные конуса Морзе

Для многих применений длина конуса Морзе оказалась избыточной. Поэтому были придуманы девять типоразмеров укороченных конусов Морзе, полученных удалением более толстой части конуса Морзе. Цифра в обозначении короткого конуса — диаметр новой толстой части конуса в мм. Российский стандарт на укороченные конуса ГОСТ 9953-82 «Конусы инструментов укороченные. Основные размеры.».

• B7 — укороченный до 14 ммКМ0 .
• B10 ,B12 — укороченный до 18 и 22 мм соответственноКМ1 .
• B16 ,B18 — укороченный до 24 и 32 мм соответственноКМ2 .
• B22 ,B24 — укороченный до 45 и 55 мм соответственноКМ3 .
• B32 — укороченный до 57 ммКМ4 .
• B45 — укороченный до 71 ммКМ5 .

Конус Морзе – это одно из самых распространенных средств для закрепления инструмента на станке. Свое название данный инструмент получил в честь знаменитого инженера Стивена Морзе, жившего в XIX веке. Сегодня для правильного выбора размеров этого изделия применяют дробные числа. Существует несколько стандартизованных значений, различающихся углами наклона и размерами.

Область применения конуса Морзе – это машиностроение. С его помощью можно быстро и очень точно закрепить режущий инструмент. Для этого конус Морзе крепится в станке в специальном отверстии или патроне, а в него в свою очередь вставляется например сверло. Такой способ крепежа гарантирует наиболее точное центрирование и последующую обработку. Также с его помощью можно подавать к обрабатываемой детали или режущему инструменту смазочно-охлаждающую жидкость.

Сечение конуса

Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.

Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.

Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.

Угол конуса

Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:

1. На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
2. Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
3. Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.

Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.

Размеры, мм

Внутренние конусы

Для конусов с лапкой

Для конусов с резьбовым отверстием

Конус	Метричес­кий	Морзе	Метрический
Обозначение конуса	4	6	1	2	3	4	5	6	80	100	120	160	200
Конусность	1 : 20 = 0,05	1 : 19,212 = 0,05205	1 : 20,047 = 0,04988	1 : 20,020 = 0,04995	1 : 19,922 = 0,05	1 : 19,254 = 0,05194	1 : 19,002 = 0,05263	1 : 19,180 = 0,05214	1 : 20 = 0,05
D	4	6	9,045	12,065	17,780	23,825	31,267	44,399	63,348	80	100	120	160	200
d5	3	4,6	6,7	9,7	14,9	20,2	26,5	38,2	54,6	71,5	90	108,5	145,5	182,5
d6	—	—	—	7	11,5	14	18	23	27	33	39	52
l5 min	25	34	52	56	67	84	107	135	188	202	240	276	350	424
l6	21	29	49	52	62	78	98	125	177	186	220	254	321	388
g	2,2	3,2	3,9	5,2	6,3	7,9	11,9	15,9	19	26	32	38	50	62
h	8	12	15	19	22	27	32	38	47	52	60	70	90	110

1. ГОСТ предусматривает размеры и для конусов инструментальных наружных.

2. Предельные отклонения размеров конусов и допуски формы по ГОСТ 2848-75.