Геометрические параметры конической зубчатой передачи - moy-instrument.ru

Типы станков для обработки конических колес

Колёса с прямыми зубьями обрабатывают, обычно, на зубодолбежных или зубострогальных станкахпо методу обкатки одним или чаще двумя резцами. На этих станках воспроизводится зацепление нарезаемого зубчатого колеса с воображаемым плоским производящим зубчатым колесом; при этом два зуба последнего представляют собой зубострогальные резцы, совершающие возвратно-поступательное движение, боковые поверхности каждого из зубьев нарезаемого зубчатого колеса формируются в результате движения резцов и обработки находящихся в зацеплении плоского и нарезаемого зубчатых колёс. Процесс нарезания зубьев происходит при движении резцов к вершине конуса заготовки, а обратный ход является холостым (в этот период резцы отводятся от заготовки).

Пример зубострогальных станков:

5236П станок зубострогальный для нарезания прямозубых мелкомодульных конических колес Ø 125
5Т23В станок зубострогальный для нарезания прямозубых прецизионных мелкомодульных конических колес Ø 125
5230 станок зуборезный для нарезания прямозубых конических колес Ø 320
5А250П станок зубострогальный для нарезания прямозубых конических колес Ø 500
526 станок зубострогальный для нарезания прямозубых конических колес Ø 610

Конические зубчатые колёса с круговыми зубьями нарезаются на зуборезных станках методом обкатки с применением зуборезной резцовой головки, представляющей собой диск с вставленными по его периферии резцами, обрабатывающими профиль зуба с двух сторон (первая половина резцов обрабатывает одну сторону, вторая половина — другую).

Пример зуборезных станков:

528С cтанок зуборезный для нарезания конических колес с круговыми зубьями Ø 800
525 cтанок зуборезный для нарезания спиральных конических колес Ø 500
5С280П станок зуборезный для конических зубчатых колес с круговыми зубъями полуавтомат Ø 800
5С23П станок зубострогальный для нарезания методом обкатки мелкомодульных конических и гипоидных колес с круговыми зубьями Ø 125

Передаточное число

Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.

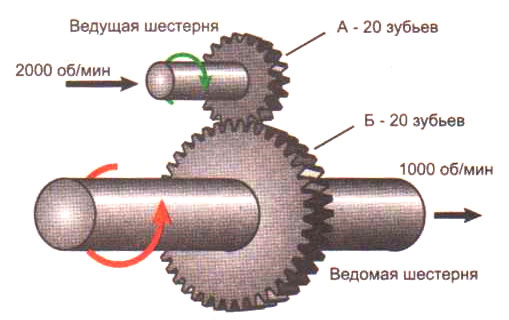
Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.

Виды механизмов передачи движения

Передачей называют техническое приспособление для передачи того или иного вида движения от одной части механизма к другой. Передача происходит от источника энергии к месту ее потребления или преобразования. Первые передаточные механизмы были разработаны в античном мире и использовались в системах орошения Древнего Египта, Междуречья и Китая. Средневековые механики значительно усовершенствовали устройства, передающие движение, и разработали множество новых видов, используя и в прялках и гончарном деле. Подлинный же расцвет начался в Новое время, с внедрением технологий производства и точной обработки стальных сплавов.

Основные геометрические параметры

Построение кинематической схемы, технические характеристики, способы обработки отдельных деталей этих механизмов задаются геометрической формой отдельных элементов. Основными геометрическими параметрами, которые рассчитываются при проектировании являются:

углы делительных конусов (каждого колеса или шестерёнки);
диаметры всех элементов (обоих валов, ведущих и ведомых шестерён);
внешний окружной модуль шестерни;
расстояние от вершины конуса до его образующей (называется делительное расстояние);
расстояние между осей;
радиальный зазор применяемых подшипников;
делительный диаметр (он определяет величину зуба шестерёнки);
диаметр углублений и верхней части зубьев.

Для удобства проведения расчетов и понимания механизма зацепления вводят три вида торцовых сечений. Это сечения во внешней, внутренней и средней части каждого зуба.

Уменьшение толщины зубьев по направлению к вершине приводит к созданию надежного зацепления во время движения. Угол наклона по направлению к вершине определяет параметры, задаваемые при обработке.

Под линией зубьев понимают пересечение двух прямых. Одна образована боковой поверхностью зуба, вторая является краем делительной конической поверхности.

Для улучшения эксплуатационных характеристик — повышения износостойкости, сопротивления при контакте, уменьшение заедания и лучшей передачи коническим зубчатым колёсам энергии вращения используют метод выравнивания коэффициентов удельного скольжения.

С этой целью колесо и шестерню стараются изготовить с одинаковыми параметрами смещения, но с разными знаками. Например, для шестерни задают параметр со знаком плюс, а для колеса со знаком минус.

Основные геометрические соотношения задаются на этапе разработки всего механизма конической передачи качество передачи. Геометрические параметры рассчитываются на основании известных соотношений.

Обслуживание

Своевременное обслуживание любой техники в соответствии с рекомендациями ее производителя обеспечит ее нормальное функционирование, паспортную производительность и выработку планового ресурса.

Обслуживание разбивается на несколько видов

текущее обслуживание;
диагностика;
планово-предупредительный ремонт;
внеплановый ремонт;
аварийный ремонт.

При условии проведения текущего обслуживания и планово-предупредительных ремонтов в соответствии с графиками удается значительно снизить риски выхода оборудования из строя.

Диагностика проводится с заданной периодичностью и призвана выявить негативные изменения в работе оборудования на ранней стадии и минимизировать потери времени и средств на внеплановые ремонты.

Обслуживание зубчатых передач заключается в их своевременной смазке.

Для ременных необходимо периодическое восстановление силы натяжения ремня.

Диагностика проводится как методом визуального осмотра, таки измерением температуры, уровня шума и вибрации, ультразвуковым и рентгеновским просвечиванием механизма без его разборки.

Обслуживание зубчатого механизма

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

https://youtube.com/watch?v=S3XcGCWR-RI

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

трение соприкасаемых поверхностей;
изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
потери на шпонках и шлицах;
трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Как рассчитать обороты шестерни простым способом

Как рассчитать передаточное отношение шестерен механической передачи.

В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев

Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев

Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.

Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.

Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.

Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.

В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.

Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.

Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.

Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.

Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.

В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.

Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.

Определим теперь частоту вращения.

Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.

Будем использовать формулу: S1 × T1 = S2 × T2,

S1 – частота вращения желтой (ведущей) шестерни,

Т1 – количество зубьев желтой (ведущей) шестерни;

S2- частота вращения красной шестерни,

Т2 – количество зубьев красной шестерни.

В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.

340 rpm × 7 = S2 × 40

Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.

Источник

Функции механических передач

Главная функция механических передач — это предать кинетическую энергию от ее источника к потребителям, рабочим органам. Помимо главной, передаточные механизмы выполняют и дополнительные функции:

Изменение числа оборотов и крутящего момента. При постоянном количестве движения изменения этих величин обратно пропорциональны. Для ступенчатого изменения применяют сменные зубчатые пары, для плавного подходят ременные или торсионные вариаторы.
Изменение направления вращения. Включает как обычный реверс, так и изменение направления оси вращения с помощью конических, планетарных или карданных механизмов.
Преобразование видов движения. Вращательного в прямолинейное, непрерывного в циклическое.
Раздача крутящего момента между несколькими потребителями.

https://youtube.com/watch?v=Bb7leiitIo4

Механические передачи выполняют и другие вспомогательные функции.

Методы регулировки и измерения параметров конических главных передач

В связи с особенностями конструкции корпуса у большинства конических главных передач ведущая шестерня устанавливается со смещением на заданную величину относительно центра опоры ведомой шестерни, а ведомая шестерня допускает исключительно регулировку зазора боковой поверхности зубьев.

У меньшей части конструкций предусматривается регулировка заданного размера смещения ведущей и ведомой шестерен, в результате которой достигается требуемый зазор боковой поверхности зубьев.

Необходимые измерительные приспособления (рис. 16 «Пример измерительного приспособления для регулировки ведущей конической шестерни«) и точные инструкции по регулировке можно запросить у производителя автомобиля.

Механические передачи

Механические передачи служит для того, чтобы передать вращение от ведущего вала к ведомому, от места генерации механической энергии (обычно — двигатель того или иного типа) к месту ее потребления или преобразования.

По методу передачи механической энергии среди передач различают следующие виды:

Виды механических передач

Зубчатые передающие механизмы, в свою очередь, подразделяются на такие виды, как:

цилиндрические;
конические;
профиль Новикова.

По соотношению скорости вращения ведущего и ведомого валов различают редукторы (снижающие обороты) и мультипликаторы (увеличивающие обороты). Современная механическая коробка передач для автомобиля объединяет в себе оба вида, являясь одновременно и редуктором, и мультипликатором.

Реечная и ременная зубчатая передача

Реечная передача преобразует вращательное движение в поступательное. Одно из зубчатых колес пары как бы развернуто в линию и представляет собой зубчатую рейку. Такой способ используется в рулевом управлений автомобиля, в других исполнительных механизмах.

Она состоит из двух закрепленных на входном и выходном валу колес-шкивов, охваченных кольцевым приводным ремнем. Вращение передается за счет сил трения, возникающих на шкивах.

Плоские и круглые ремни используются при небольших нагрузках. Широкое распространение получил ремень в форме клина, шкив при этом выполняется со щечками, и зацепление осуществляется одной нижней и двумя боковыми поверхностями ремня.

Ремни также снабжаются зубчатыми фрагментами. Поликлиновые передачи широко применяются в современных автомобильных и мотоциклетных вариаторах. Они позволяют передавать значительный крутящий момент и плавно регулировать скорость вращения ведомого вала.

Преимущества и недостатки ремённых передач

Как и у любого устройства, у ремённой передачи есть свои плюсы и минусы по сравнению с другими механизмами. Выделим важные из них.

Преимущества:

простота конструкции;
малая стоимость:
малая шумность;
плавность работы;
сглаживание ударных перегрузок за счет упругости ремня;
возможность менять направление вращения под разным углом;
возможность передавать вращение на большое расстояние.

Недостатки:

большие габариты конструкции;
плохая работа на больших скоростях (появление вибраций);
большая нагрузка на оси (валы, подшипники);
непостоянное передаточное отношение при разной нагрузке (из-за упругого скольжения);
малый срок службы ремня по сравнению с зубчатыми колесами;
биение приводного ремня при его слабом натяжении;
необходимость в дополнительных элементах при большой длине ремня или малом угле обхвата;
увеличение износа приводного ремня или осей при неправильном натяжении.

Волновая зубчатая передача

Принцип действия

Состоит из жёсткого неподвижного элемента — зубчатого колеса с внутренними зубьями, неподвижного относительно корпуса передачи; гибкого элемента — тонкостенного упругого зубчатого колеса с наружными зубьями, соединённого с выходным валом; генератора волн — кулачка, эксцентрика или другого механизма, растягивающего гибкий элемент до образования в двух (или более) точках пар зацепления с неподвижным элементом. Число зубьев гибкого колеса несколько меньше числа зубьев неподвижного элемента. Число волн деформации равно числу выступов на генераторе. В вершинах волн зубья гибкого колеса полностью входят в зацепление с зубьями жёсткого, а во впадинах волн — полностью выходят из зацепления. Линейная скорость волн деформации соответствует скорости вершин выступов на генераторе, то есть в гибком элементе существуют бегущие волны с известной линейной скоростью. Разница чисел зубьев жёсткого и гибкого колёс обычно равна (реже кратна) числу волн деформации.

Например, при числе зубьев гибкого колеса 200, неподвижного элемента — 202 и двухволновой передаче (два выступа на генераторе волн) при вращении генератора по часовой стрелке первый зуб гибкого колеса будет входить в первую впадину жёсткого, второй — во вторую и т.д. до двухсотого зуба и двухсотой впадины. На следующем обороте первый зуб гибкого колеса войдёт в двести первую впадину, второй — в двести вторую, а третий — в первую впадину жёсткого колеса. Таким образом, за один полный оборот генератора волн гибкое колесо сместится относительно жёсткого на 2 зуба.

Достоинства

большое передаточное отношение, при малом количестве деталей (i = 80-320)
улучшенные массо-габаритные характеристики по сравнению с обычными зубчатыми передачами
высокая кинематическая точность и плавность хода
высокая нагрузочная способность
передача момента через герметичные стенки

Достоинства и недостатки

Применение данной кинематической схемы наглядно показало наличие преимуществ.

К положительным моментам можно отнести:

способность изменять направление передаваемого движения;
широкая область применения;
эффективно реализована передача, преобразование, увеличение мощности вращательного движения между осями передачи расположенными под углом друг к другу;
достаточно широкий диапазон задания углов передачи крутящего момента от ведущего элемента к ведомому;
широкая вариативность при компоновке разрабатываемых зубчатых и комбинированных систем;
высокие нагрузочные характеристики (данные устройства способны передавать мощность величиной до 5000 кВт);
эксплуатация и обслуживание не вызывает трудностей;
удаётся получить высокий КПД.

К недостаткам специалисты причисляют:

нагрузочная способность ниже, чем у цилиндрических конструкций (в среднем она на 20 процентов ниже);
невысокая несущая способность (этот показатель ниже на 15 процентов);
сложность и трудоёмкость в изготовлении колёс с заданными параметрами зубьев (количеством, величиной, углом наклона);
повышенные требования к точности нарезания зубьев;
возникновение повышенных осевых и изгибных нагрузок на все валы (особенно этот эффект наблюдается между валами, расположенными консольно);
необходимость регулировки процесса передачи вращения;
обладают большей массой, чем другие зубчатые передачи;
высокие затраты на производство и обслуживание;
возникают трудно разрешимые проблемы при проектировании и изготовлении систем с изменяемым передаточным числом;
повышенная общая жёсткость конструкции.

Основные показатели для выбора механических передач

Выбор типа передачи — сложная конструкторская задача. Нужно подобрать вид и спроектировать механизм, наиболее полно удовлетворяющий техническим требованиям, сформулированным для данного узла.

При выборе конструктор сопоставляет следующие основные факторы:

опыт предшествующих аналогичных конструкций;
мощность и момент на валу ;
число оборотов на входе и на выходе;
требуемый К.П.Д.;
массогабаритные характеристики;
доступность регулировок;
плановый эксплуатационный ресурс;
себестоимость производства;
стоимость обслуживания.

При высоких передаваемых мощностях обычно выбирают многопоточный зубчатый вид. При необходимости регулировки числа оборотов в широком диапазоне разумно будет выбрать клиноременной вариатор. Конечное решение остается за конструктором.

Устройство конической передачи

Коническая зубчатая передача представляет собой пару конических шестерен — зубчатых колес, прошедших обработку под заданным углом. После обработки обе шестерни получают изменяемый от основания к вершине диаметр, форму, напоминающую конус, благодаря чему и получили свое название. Зубья шестерен вырезаются на боковой поверхности, при работе конические шестерни сопрягаются боковыми плоскостями. Конические пары в силу особенностей своей конструкции считаются наиболее сложными в изготовлении и сборке. К тому же они имеют не самую высокую несущую способность (например, у конической передачи при прочих равных параметрах она на 15% ниже). Тем не менее в узлах и механизмах, где необходима передача крутящего момента с угловым смещением, альтернативы им нет. Элемент пары, передающий крутящий момент, называют ведущим (шестерней), а тот, что принимает крутящий момент — зубчатым колесом (ведомым). Результирующий угол изменения направления вращения равен сумме углов обеих конических шестерен. Наиболее часто в машинах и механизмах встречается ортогоническая коническая пара, изменяющая направление вращающего момента под углом 90 градусов (2 х45). Возможности конической передачи не исчерпываются способностью изменять направление оси вращения в широком диапазоне углов. С помощью такой конструкции можно также изменить частоту вращения (число оборотов в минуту) и мощность.

Передаточное отношение зубчатой передачи

Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.

При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.

Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.

Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.

Передаточное отношение редуктора вычисляется по формуле:

где U₁₂ – передаточное отношение шестерни относительно колеса;

ω₁ и ω₂ – угловые скорости ведущего и ведомого элемента соединения;

Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Источник

Конические зубчатые колеса

Прежде чем приступить к выполнению чертежа конического зубчатого колеса, необходимо иметь следующие данные:

φ – Угол наклона образующей начального конуса к его оси.d – Диаметр начальной окружности или модуль m зацепления.z – Число зубьев.b – Длину зуба.
При вычерчивании конического зубчатого колеса с натуры угол φ можно определить следующим приемом:

1) при помощи угломера определяем угол а, сторонами которого являются контурные образующие дополнительного конуса

₁_e_e_e

1) измеряют диаметр D_e выступов и диаметр D_i впадин (фиг. 535), вычитают из первого второй.

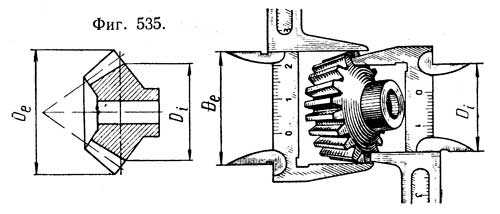
2) так как отношение высоты h’ головки зуба к высоте h” ножки зуба составляет 1 : 1,2 или 5 : 6, получившуюся разность между диаметрами делят на общее число частей, т. е. на 5 + 6 = 11 частей (для конических колес высоту h” ножки зуба принимают равной 1,2m).
Для нахождения величин d надо или прибавить к D_i шесть таких частей или вычесть из D_e пять таких частей:

d=Di+6((De-Di)÷11) или d = De – 5((De-Di)÷11)

Модуль m зацепления определяем из формулы m = d ÷ z полученное значение модуля согласовываем со стандартом и в случае несовпадения берем ближайшее большее значение m и вновь пересчитываем диаметр d. Угол φ можно определить без угломера следующим образом:

D_e = d + 2m cos φ; 2m cos φ = D_e – d;
cos φ = (D

e – d) ÷ 2m

Отсюда определяем значение угла φ.

Одноступенчатые цилиндрические редукторы

Этот тип редуктора отличается от прочих положением валов в корпусе и числом ступеней. Одноступенчатые цилиндрические редукторы могут быть вертикальными и горизонтальными. Шестеренки этих устройств могут иметь косые и прямые, а также шевронные зубья. Корпуса производят из стали сварным способом или из чугуна путем литья. Монтаж валов зачастую производится в подшипники скольжения или качения. Первые зачастую устанавливаются в тяжелых редукторах.

Это интересно: Неисправности ДАД

Состав и возможности компоновки одноступенчатого редуктора ограничены. Главной чертой, которая отличает их друг от друга, является расположение валов и осей в пространстве. При этом передаточное число этих агрегатов колеблется в диапазоне от 1,6 до 6,3. Угол наклона передач, выполненных с использованием косозуба, находится в диапазоне от 8 до 200 градусов.

Максимальное передаточное число, которые способен обеспечить агрегат равно 12,5, но при этом редукторы с максимальным передаточным числом применяются редко. Зачастую используются те, которые имеют передаточное число, не превышающее цифру 6.

Какое расположение редуктора выбрать — вертикальным или горизонтальным? Все зависит от необходимости удобств общей компоновки этого передаточного устройства. В частности имеет значение, как расположен агрегат, который производит механическое движение, его рабочий вал и т.д.

Особенности зубчатого механизма

Ременная передача предполагает наличие между шкивами на связанных валах промежуточного звена – гибкого ремня. Зубчатый механизм от такого соединения отличается наличием на поверхности сопряженных деталей зубьев зацепления. По профилю и размеру они идентичны.

Головка зуба колеса входит в зацепление с повторяющей ее профиль впадиной на шестерне. При вращении ведущего вала ведомый проворачивается в противоположную сторону. Между ними конструктивно предусмотрен минимально возможный зазор, обеспечивающий скольжение, тепловое расширение и смазку для недопущения заклинивания. При этом ведущая часть парного механизма называется колесом, а ведомая – шестерней.

У ременной передачи плоскость зацепления ремня со шкивом составляет не менее трети длины окружности. В зубчатом механизме между ведущим колесом и ведомой шестерней под нагрузкой в постоянном контакте находится одна пара зубьев. Колеса и шестерни на валах обычно монтируются на шпоночном соединении.