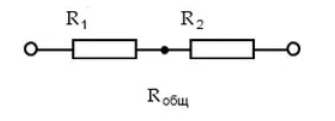
Последовательное соединение пружин : жесткость, формула

Как определить жесткость системы при последовательном соединении пружин?

Довольно большое количество проблем возникает на момент вычисления жесткости системы при последовательном соединении. Особенностями проводимого расчета в этом случае назовем следующее:

Важным показателем можно назвать жесткость, которая варьирует в достаточно большом диапазоне. Она во многом определяет свойства изделия. При слишком большой жесткости приходится прикладывать большее усилие для растяжения или сжатия детали.
Телу придается определенное усилие (F), которое становится причиной удлинения тела на величину x.
Для расчета применяется формула: k=»F/(2x)=1/2F/x=k/2.

Приведенная» выше информация указывает на то, что жесткость всей системы в этом случае в два раза меньше показателя жесткости каждого изделия. При этом формула применима только в том случае, если применяемые варианты исполнения для соединения обладают одинаковыми эксплуатационными характеристиками.

Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система двух пружин получила весьма широкое распространение, так как при ее применении можно добиться требующихся результатов. Однако, прежде чем ее использовать следует провести соответствующие расчеты.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Чем отличаются параллельное и последовательное подключения

Последовательное подключение представляет собой последовательное соединение проводников в одной общей электрической цепи.

Почему оно последовательное?

Всё очень просто – проводники располагаются в электрической цепи аналогично птицам, которые сидят на проводе – один за другим. В данном случае представим, что птицы держатся за лапы – каждая птица держит своей левой лапой правую лапу ближайшей птицы. Получаем ёлочную гирлянду. Все сидят последовательно.

Кстати говоря, если свободные лапы крайних птиц прислонить к источнику питания, то выйдет фейерверк :)…

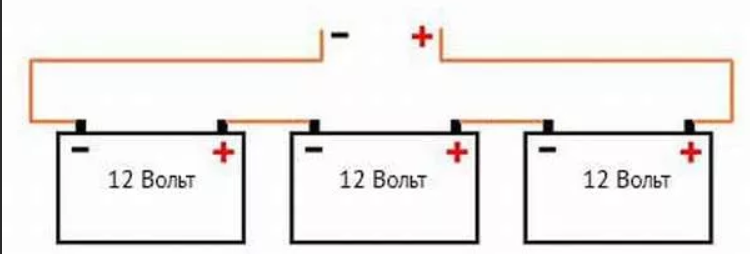
Представим, например, светодиод, который имеет + и -. Для того, чтобы объединить такие светодиоды в единую последовательную цепь, мы должны соединить ножку + первого светодиода с плюсом источника постоянного тока, а ножку – соединить с ножкой + следующего светодиода. Ножку – следующего светодиода мы подключаем также к ножке + следующего светодиода, а – подключаем к – источника постоянного тока. Вот мы и собрали простейшую последовательную цепь из трех элементов.

Параллельное подключение выглядит немного иначе.

Если вернуться к примеру с птицами, то птицы уже не сидят на проводе одна за другой, а держат друг друга лапами.

Причем, птицы так извернулись, что одна птица держит своей правой лапой, правую лапу соседней птицы, а левой лапой левую лапу этой же птицы.

Для того, чтобы зажарить таких птиц, остаётся только прислонить букет из этих соответствующих друг другу лап к полюсам источника тока.

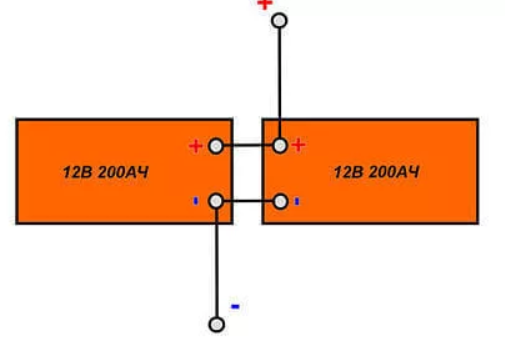
Здесь мы берем, скажем, два светодиода, которые имеют ножки + и – соответственно, и соединяем сначала ножки светодиодов по принципу + к + и – к -.

Собранную цепь мы подключаем к источнику тока соответственно полюсам, т.е. общий плюс от двух светодиодов присоединяем к + источника тока, а общий – к минусу источника тока. В результате получили параллельную цепь.

Смешанное соединение сочетает в себе как параллельное, так и последовательные соединения. В зависимости от цели, эти комбинации могут быть различными.

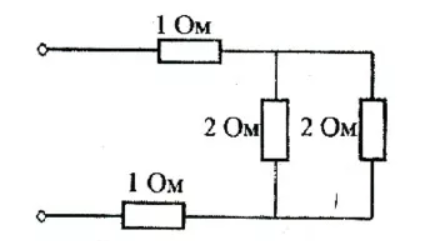
На практике чаще всего используются именно смешанные схемы. Часто анализ такого соединения вызывает затруднения у студентов и школьников.

На самом же деле, тут нет ничего сложного.

Для того, чтобы разобраться во всех параметрах, нужно попросту разложить цепь на удобные фрагменты.

Так, если мы имеем ряд последовательно подключенных резисторов, которые скомпонованы вместе с параллельно соединенными резисторами, то цепь можно разбить на два обобщенных условных участка, где и определить значимый параметр.

Часто испуг вызывает появление в схеме поворотов, углов и изгибов. Человек теряется и не понимает, что от смены направления линии соединительных проводов, логика не меняется.

Сила упругости в пружинном маятнике

Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.

Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:

Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.

Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.

О понятии жесткости. Жесткость пружины: формула

Определение

Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.

Посмотрите на закон Гука.

Формула

Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.

k – это и есть жёсткость пружины.

Fупр — сила жесткости или упругости пружины.

x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.

Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.

Закон Гука является одним из основных законов физики.

Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:

Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.

Имеем два уравнения:

Т. к. Fупр =Fтяж, получаем

Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна

Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Как рассчитать жесткость цилиндрической пружины

В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.

С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.

Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.

Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.

Окончательная формула для жёсткости цилиндрической пружины такова:

Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.

Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.

Анна Краснова – Бакалавр физики

Умеешь писать статьи?Разбираешься в теме?

Начни писать статьи на заказ!

Расчет пружины сжатия из проволоки прямоугольного сечения

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.

Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C 1 ) , задающей жесткость пружины (C ) в целом.

Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.

После выполнения расчета по программе выполняйте проверку касательных напряжений!!!

4. I =(D 1 B ) -1

5. При 1/3 Y =5,3942*(H B ) 2 -0,3572*(H /B )+0,5272

При 1 Y =5,4962*(H B ) (-1.715)

При 2H B Y =3 ,9286 *(H B ) (-1. 2339 )

6. При H B C 1 =(78500* H 4 )/(Y * (D 1 — B ) 3)

При H > B C 1 =(78500* B 4 )/(Y * (D 1 — B ) 3)

8. T nom =1,25*(F 2 C 1 )+H

9. T max =π*(D 1 — B )*tg (10 ° )

11. S 3 = T — H

12. F 3 = C 1 * S 3

14. N расч =(L 2 — H )/(H +F 3 C 1 — F 2 C 1 )

16. C = C 1 N

17. L 0 = N * T + H

18. L 3 = N * H + H

19. F 2 = C * L 0 — C * L 2

21. F 1 = C * L 0 — C * L 1

22. N 1 = N +1,5

23. A =arctg (T /(π *(D 1 — H )))

24. L разв =π* N 1 *(D 1 — H )/cos (A )

25. Q =H *B * L разв *7,85/10 6

Это интересно: Конденсатор для пуска электродвигателя, как рассчитать мощность — во всех подробностях

Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.

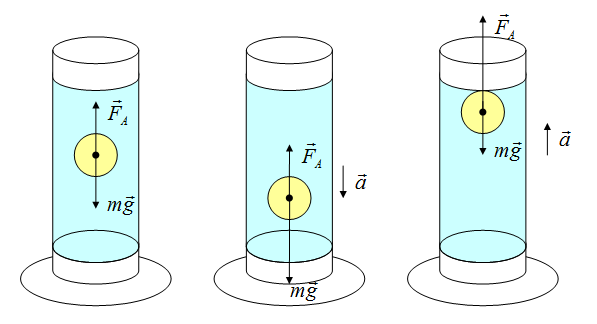
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как Сила Кулона, сила Ампера, сила Лоренца.

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Локальная система отсчёта

— это система отсчёта, которая может считаться инерциальной, но лишь в бесконечно малой окрестности какой-то одной точки пространства-времени, или лишь вдоль какой-то одной незамкнутой мировой линии.

Преобразования Галилея. Принцип относительности в классической механике.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система Kбудет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+vt;y=y’;z=z’;t=t’, названных преобразованиями Галилея.Механический принцип относительности.Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.Нарушение классического закона сложения скоростей.Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x’=(x-vt)/(1-v 2 /c 2 ); y’=y; z’=z; t’=(t-vx/c 2 )/(1-v 2 /c 2 ). Эти преобразования называются преобразованиями Лоуренса.

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Физика

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

Потенциальная энергия деформированной пружины

Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенциальной энергией, которая определяется формулой

W p = k ( Δ l ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

Wp = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

W p = k общ ( Δ l ) 2 2 ,

где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

для N одинаковых пружин, соединенных последовательно,

k общ 1 = k 0 N ;

для N одинаковых пружин, соединенных параллельно,

kобщ2 = Nk0,

где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;

для N одинаковых пружин, соединенных параллельно,

W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .

Отношение потенциальных энергий

W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;

соединенных параллельно:

W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.

Отношение указанных потенциальных энергий равно

W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

Wp = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h2 + h2,

где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

Wp = mg(h2 + h2).

Расчет дает значение:

W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.

Деформации и силы упругости

Определение 1 Силой упругости называется такая сила, которая возникает при деформации вещества и стремится вернуть его в первоначальное состояние.

На все тела вокруг нас действуют различные деформации. Они появляются из-за движения тел и изменения относительного расположения их частичек. В зависимости от степени обратимости процесса деформации, различают упругие и пластические (остаточные) деформации, или, другими словами, обратимые и необратимые.

Упругой называется такая деформация, при которой тело по окончанию воздействия силы, приводящей к деформации, возвращается в первоначальное положение и сохраняет свои первоначальные параметры.

Упругая деформация возможна лишь в том случае, когда сила внешнего воздействия не больше, чем предел упругости. Другими словами, сила упругости компенсирует воздействие на тело внешней силы.

Если же воздействие внешней силы превышает предел упругости, происходит пластическая или остаточная деформация. То есть, после воздействия такой силы тело теряет свои первоначальные параметры.

Явление пластической деформации обусловлено тем, что возникающие в теле упругие силы не способны полностью противостоять воздействиям внешних сил.

Выделяют несколько видов простых деформаций:

деформация растяжения;
деформация изгиба;
деформация сдвига;
деформация кручения.

Обычно процесс деформации включает в себя совокупность нескольких таких типов одновременно, в результате этого выделяют два основных вида деформации: растяжение и сдвиг.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Решение задач Контрольные работы Эссе

Особенности расчета жесткости соединений пружин

Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.

При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.

При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.

Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.

Пружина – упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

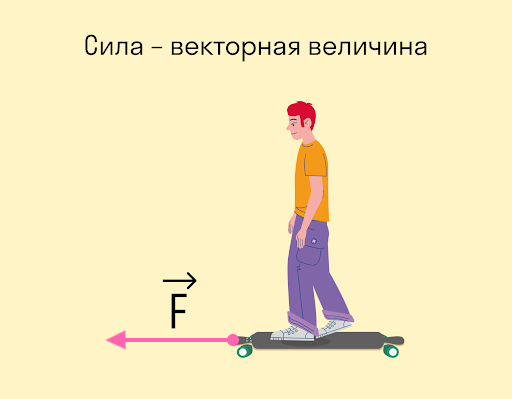
Принципы деформации

Когда сила воздействует на материал, он растягивается или сжимается в ответ. В механике сила, приложенная на единицу площади, является тем, что называется напряжением. Степень растяжения и сжатия, возникающая, когда материал реагирует на напряжение, называется деформацией. Напряжение измеряется отношением разницы в длине к исходной длине в направлении напряжения.

Каждый материал по-разному реагирует на стресс, и детали этой реакции важны для инженеров, выбирающих материалы для своих конструкций и машин, которые должны вести себя предсказуемо при ожидаемых напряжениях.

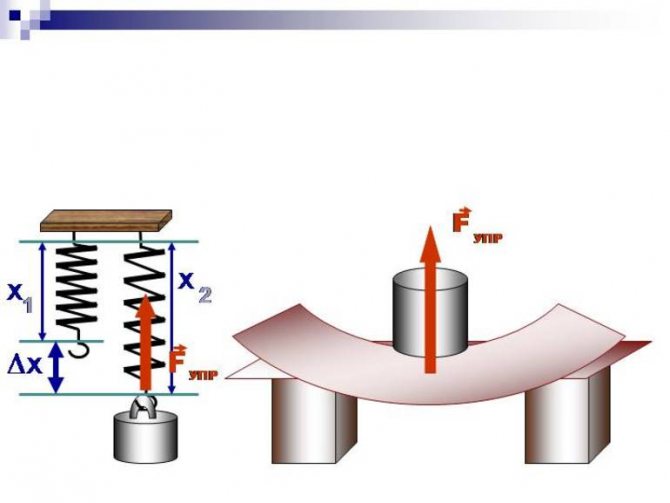
Для большинства материалов нагрузка, испытываемая при приложении небольшого напряжения, зависит от плотности химических связей. То же самое относится к жёсткости материала, которая напрямую связана с его химической структурой.

Происходящее при снятии напряжения зависит от того, насколько далеко перемещены атомы.

В целом существует два типа деформации:

Упругая. После снятия напряжения материал возвращается к размеру, который был до приложения нагрузки. Деформация обратима, непостоянна.
Пластическая. Напряжение настолько велико, что при снятии нагрузки материал не возвращается к своему предыдущему размеру. Минимальное значение напряжения, вызывающего пластическую деформацию, известно как предел упругости материала.

Пружина постоянного усилия:

Пружина постоянной силы устанавливается на барабан, оборачивая его вокруг барабана. Пружина должна быть плотно обернута. Затем свободный конец пружины прилагается к силе нагрузки, например, при использовании противовеса или наоборот.

Диаметр барабана должен быть больше внутреннего диаметра.
Диапазон: 10-20% диаметра барабана> Внутренний диаметр.
На барабане при крайнем растяжении должна быть полуторная пружина.
Полоса будет нестабильной на больших расширениях, поэтому рекомендуется использовать ее меньшего размера.
Диаметр шкива должен быть больше исходного диаметра.

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$R$ — радиус цилиндра пружины,
$n$ — количество витков проволоки радиуса $r$,
$G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^<10>$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков — 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac<Н><м>$

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Заключение.

Значение модуля сдвига (G ) материала проволоки в существенной мере влияющее на жесткость пружины (C) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.

Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…

ПрошуУВАЖАЮЩИХтруд автора скачать файлПОСЛЕ ПОДПИСКИна анонсы статей.

ОСТАЛЬНЫМ можно скачать просто так… – никаких паролей нет!

Определение

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.

Чаще всего ее обозначают ${\overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

Рассмотрим пружину, на которую действует растягивающая сила ($\overline{F}$), которая направлена вертикально вниз (рис.1).

Силу $\overline{F\ }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${\overline{F}}_u$), уравновешивающая силу $\overline{F\ }$. Если деформация является небольшой и упругой, то удлинение пружины ($\Delta l$) прямо пропорционально деформирующей силе:

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

\=\frac{\left}{\left}=\frac{Н}{м}.\]

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.