7.2. Поверхности вращения
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
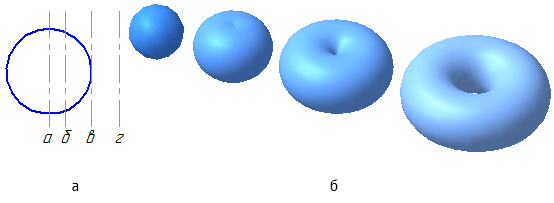
Рисунок 7.4 – Образование поверхностей вращения
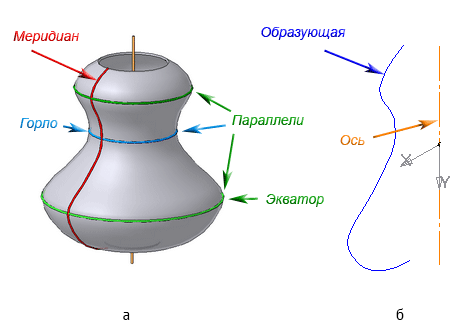
Рисунок 7.5 – Элементы поверхности вращения
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом , наибольшая – экватором .
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом .
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом .
Краткие теоретические сведения
Поверхность, допускающая параметризацию вида:
\begin{equation*}
\vec{R}=\vec{\rho}(u)+v\vec{\mu}(u),
\end{equation*}
где $\vec{\rho}$, $\vec{\mu}$ — гладкие вектор-функции,
называется линейчатой.
$u=\mbox{const}$ называется образующей (образующая имеет направляющий вектор $\vec{\mu}(u)$),
$\vec{\rho}=\vec{\rho}(u)$ называется направляющей.
Линейчатая поверхность — поверхность, описанная движением прямой, называемой образующей, пересекающей при движении некоторую кривую, называемую направляющей поверхности.
Рассмотрим два вида линейчатой поверхности — цилиндрическая и коническая.
Цилиндрическая поверхность:
Направляющая: $\vec{\rho}=\vec{\rho}(u)$,
Образующая: постоянный единичный вектор $\vec{\mu}=\vec{e}$.
\begin{equation*}
\vec{R}=\vec{\rho}(u)+v\vec{e}.
\end{equation*}
Коническая поверхность:
Вершина в точке $M(\vec{\rho}_0)$,
Направляющая: $\vec{\rho}=\vec{\rho}(u)$,
Образующая: $\vec{\mu}=\vec{\rho}(u)-\vec{\rho}_0$.
\begin{equation*}
\vec{R}=\vec{\rho}_0+v(\vec{\rho}(u)-\vec{\rho}_0).
\end{equation*}
Описанные линейчатые поверхности являются развертывающимися, то есть их касательные плоскости остаются неизменными вдоль прямолинейной образующей.
Еще один пример развертывающейся поверхности — поверхность, образованная касательными к некоторой кривой.
Из сказанного выше следует, что совокупность всех касательных плоскостей развертывающейся линейчатой поверхности представляет собой однопараметрическое семейство, то есть развертывающаяся линейчатая поверхность является огибающей однопараметрического семейства плоскостей.
Поверхность вращения — поверхность, образованная при вращении некоторой кривой около оси. Линии пересечения поверхности с плоскостями, проходящими через ось вращения, называются \emph{меридианами}, а линии пересечения с плоскостями, перпендикулярными оси, называются \emph{параллелями}.
Уравнение поверхности вращения, которая образуется при вращении кривой
\begin{equation*}
x=x(u), \,\, z=z(u), \,\, x\geqslant0
\end{equation*}
расположенной в плоскости $(xz)$, вокруг оси $Oz$:
\begin{equation*}
x=x(u)\,\mbox{cos}\,v, \,\, y= x(u)\,\mbox{sin}\,v, \,\, z=z(u).
\end{equation*}
Линейчатые поверхности. Принадлежность линии и точки к поверхности
Линейчатой называется поверхность, образующей которой является прямая линия.
В общем случае линейчатая поверхность однозначно определяется тремя направляющими линиями .
Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этойповерхности. Для задания поверхности достаточно иметь проекции направляющей линии и указать, как строится образующая прямая, проходящая через любую точку направляющей. Однако, для придания наглядности изображения, вычерчивают очерк, линии видимости и строят точки на поверхности.
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некоторой кривой направляющей линии. Если направляющей линией является окружность, то поверхность называется наклонным или эллиптическим конусом.
На рис. 3.10 представлены: направляющая окружность – m; неподвижная точка – S; прямолинейная образующая — l . Это первая часть определителя – геометрическая. Образующая движется по направляющей, оставаясь неподвижной в точке S. Описание закона движения является алгоритмической частью определителя. При этих условиях поверхность на чертеже считается заданной. Для придания наглядности, на рис. 3.11 построены очертания поверхности, линии видимости и промежуточная точка, принадлежащая поверхности.
Построение точек, принадлежащих поверхности, осуществляется следующим образом. Пусть задана фронтальная проекция точки А (А»). На фронтальной плоскости она изображена как невидимая. Для построения ее горизонтальной проекции через точку задаем линию, принадлежащую поверхности. Этой линией будет окружность, так как линия задана параллельно основанию, а основанием является окружность. Центр окружности лежит на осевой линии поверхности. Проводим линию связи из центра окружности на горизонтальную плоскость до пересечения с горизонтальной осевой поверхности. Строим окружность, которой принадлежит точка А.. По линии связи отмечаем ее местоположение с учетом видимости для горизонтальной плоскости, где точка является видимой. Аналогичные построения выполняются для наклонного (эллиптического) цилиндра.
Тема 4
Позиционные задачи
Все задачи начертательной геометрии условно могут быть разделены на метрические и позиционные. К метрическим задачам относятся задачи на измерение линейных и угловых величин. Решение этих задач будет рассмотрено ниже.
К позиционным задачам относятся задачи на принадлежность и взаимное пересечение геометрических фигур. По существу решение позиционных задач сводится к нахождению точек одновременно принадлежащих двум или более фигурам. Задачи на определение принадлежности одной геометрической фигуры к другой частично уже рассмотрены:
o принадлежность точки к прямой (рис. 1.23) .
o принадлежность линии к поверхности. Рис. 3.9 ;
o принадлежность точки к поверхности. Рис. 3.11
Задачи на построение линий пересечения геометрических фигур условно можно разделить на три группы:
o пересечение плоскости с поверхностью;
o пересечение прямой линии с плоскостью и с поверхностью.
o взаимное пересечение поверхностей.
Решение всех типов позиционных задач на пересечение подчиняются общему алгоритму. На рис. 4.1 представлена поверхность полусферы и усеченного конуса. Для построения точек, одновременно принадлежащих этим поверхностям, воспользуемся общим алгоритмом.
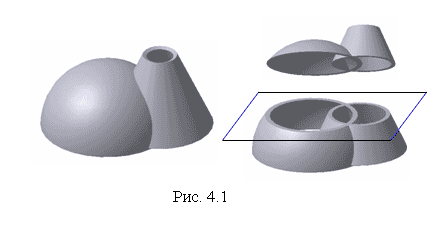
1. Вводится вспомогательная поверхность, в частном случае — плоскость. Эта вспомогательная поверхность назначается таким образом, чтобы она пересекла обе фигуры по простым для построения линиям — по прямым или по окружностям.
2. Строятся линии пересечения вспомогательной поверхности с каждой из заданных фигур.
3. Отмечаются точки взаимного пересечения построенных линий. Эти точки принадлежат обеим фигурам, следовательно, являются элементом пересечения фигур.
4. Соединяют точки в определенной последовательности и определяют видимость линии пересечения и фигур друг относительно друга.
Находить точки для построения линии взаимного пересечения фигур надо в определенной последовательности.
1. В первую очередь отмечают точки на контурных образующих или на ребрах, если поверхностигранные.
2. Находят экстремальные точки: наивысшую; наинизшую; самую левую; самую правую; самую ближнюю и самую дальнюю.
3. Отмечают точки на линиях среза (принадлежащие основаниям).
4. Если построенных точек недостаточно для выявления формы линии взаимного пересечения, строят ряд промежуточных (случайных) точек.
голоса
Рейтинг статьи
7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
Презентация на тему: » Линейчатые поверхности Образование поверхностей. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по.» — Транскрипт:
1
Линейчатые поверхности Образование поверхностей

2
Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим

3
Цилиндрическая поверхность m (m; S ) S // Цилиндрическая поверхность образуется движением прямой (образующей) по некоторой кривой m параллельно самой себе или имеющей постоянное направление S
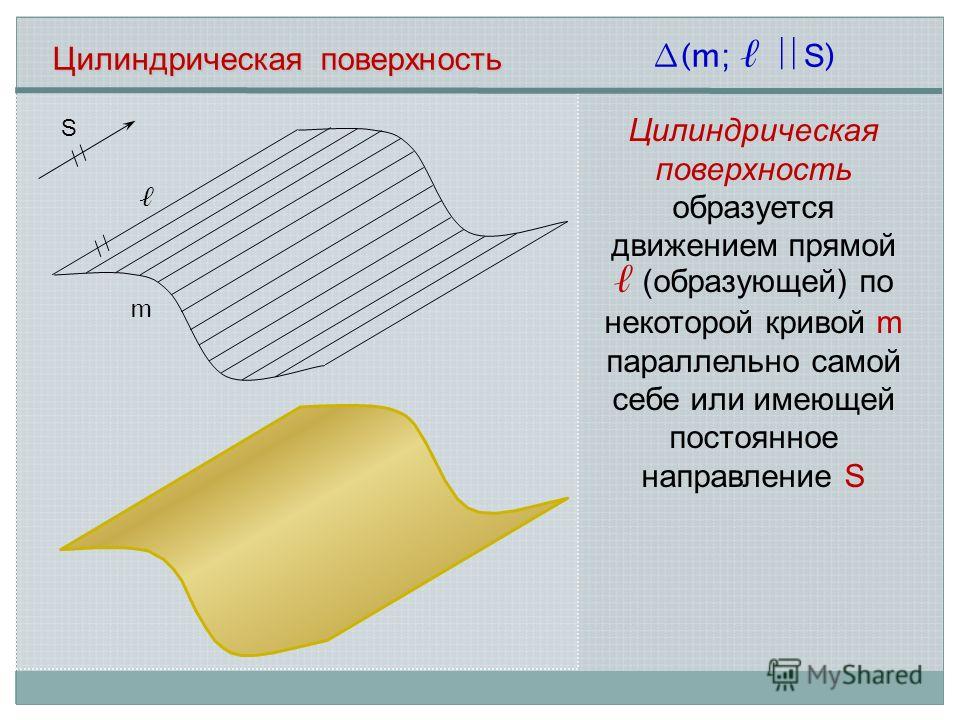
4
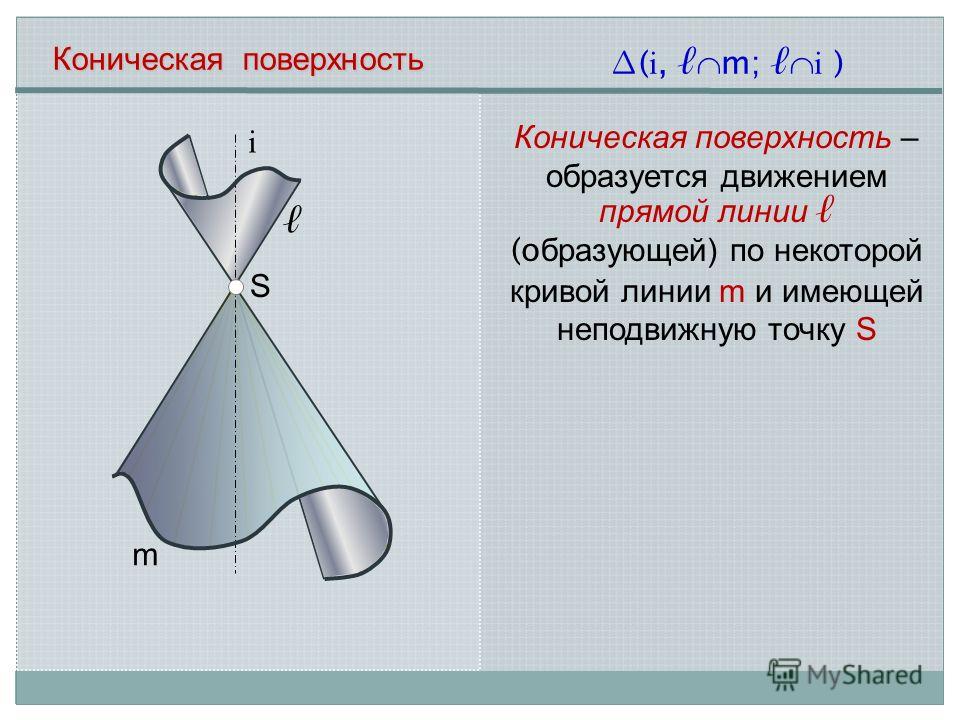
i m ( i, m; i ) Коническая поверхность Коническая поверхность – образуется движением прямой линии (о бразующей) по некоторой кривой линии m и имеющей неподвижную точку S S
5
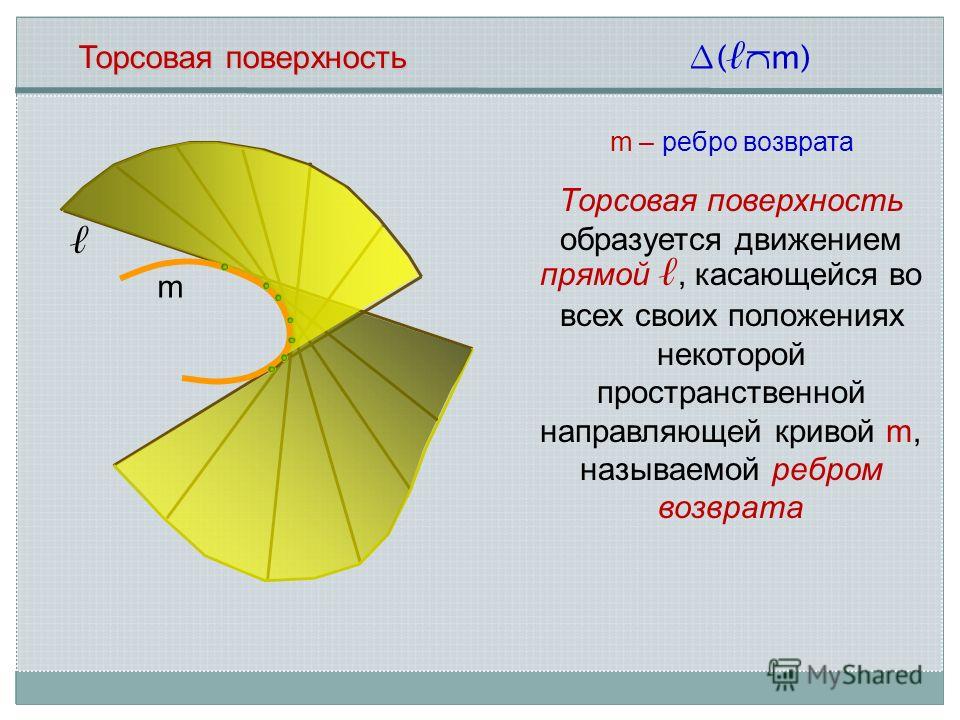
Торсовая поверхность m m – ребро возврата ( m) Торсовая поверхность образуется движением прямой, касающейся во всех своих положениях некоторой пространственной направляющей кривой m, называемой ребром возврата
6
Однополостный гиперболоид
7
Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников Отсеки плоскостей называются гранями, а линии их пересечения – ребрами Точки пересечения ребер называются вершинами

8
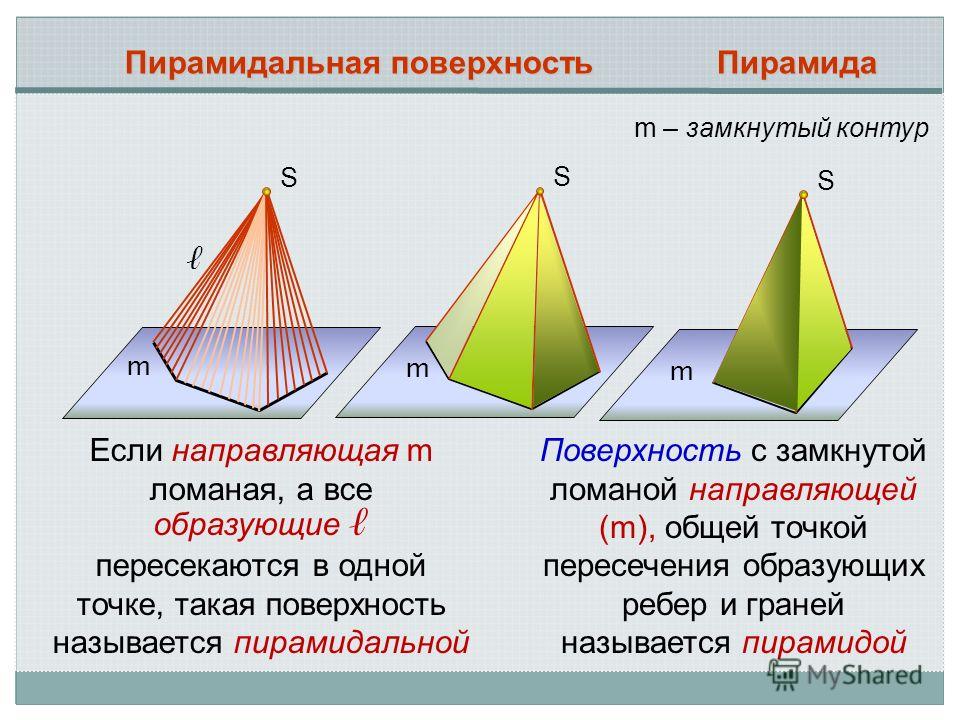
S m S m Пирамидальная поверхность S m Пирамида m – замкнутый контур Если направляющая m ломаная, а все образующие пересекаются в одной точке, такая поверхность называется пирамидальной Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой
9
Принадлежность точки поверхности

10
S А1А1 С1С1 В1В1 S2S2 X 1,2 S1S1 А2А2 С2С2 В2В2 Задача Построить недостающую проекцию точки N N2N2 N1N1
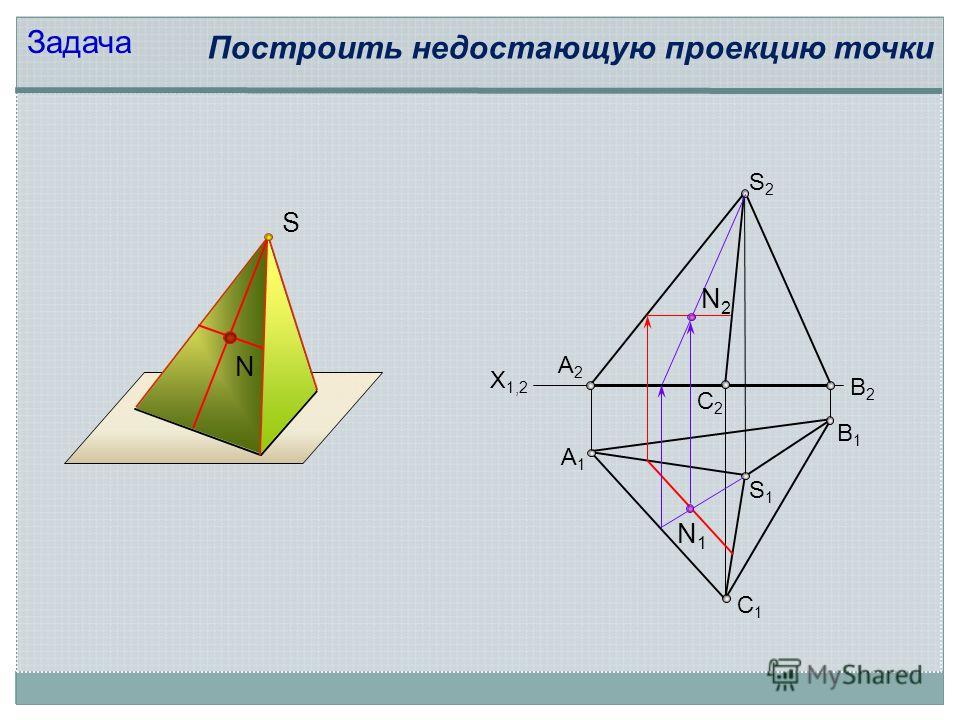
11
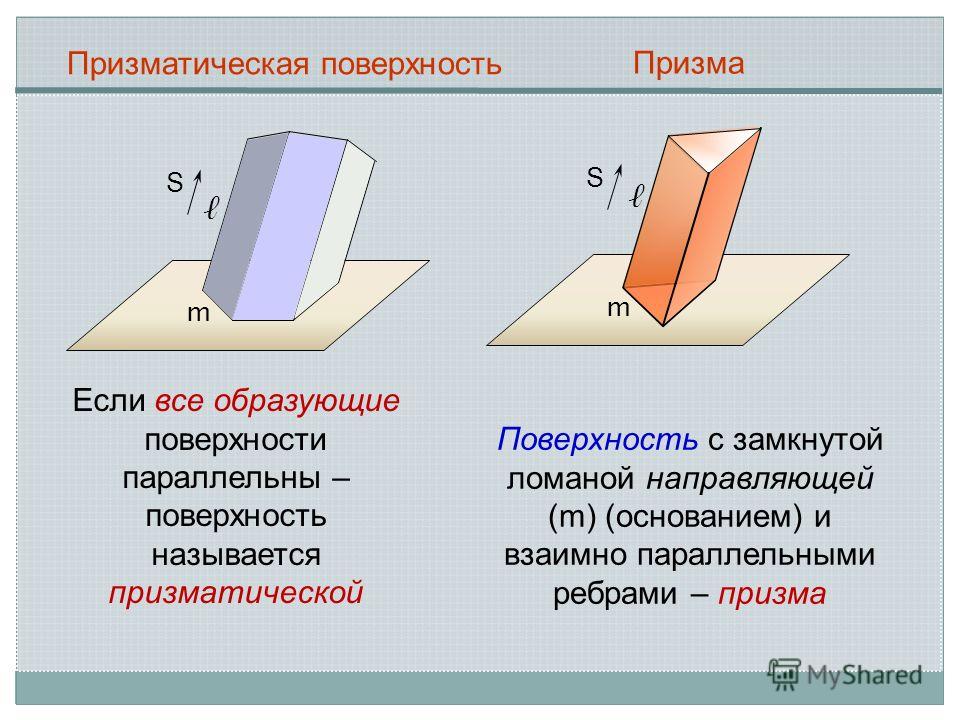
m S Призматическая поверхность m S Призма Если все образующие поверхности параллельны – поверхность называется призматической Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами – призма
12
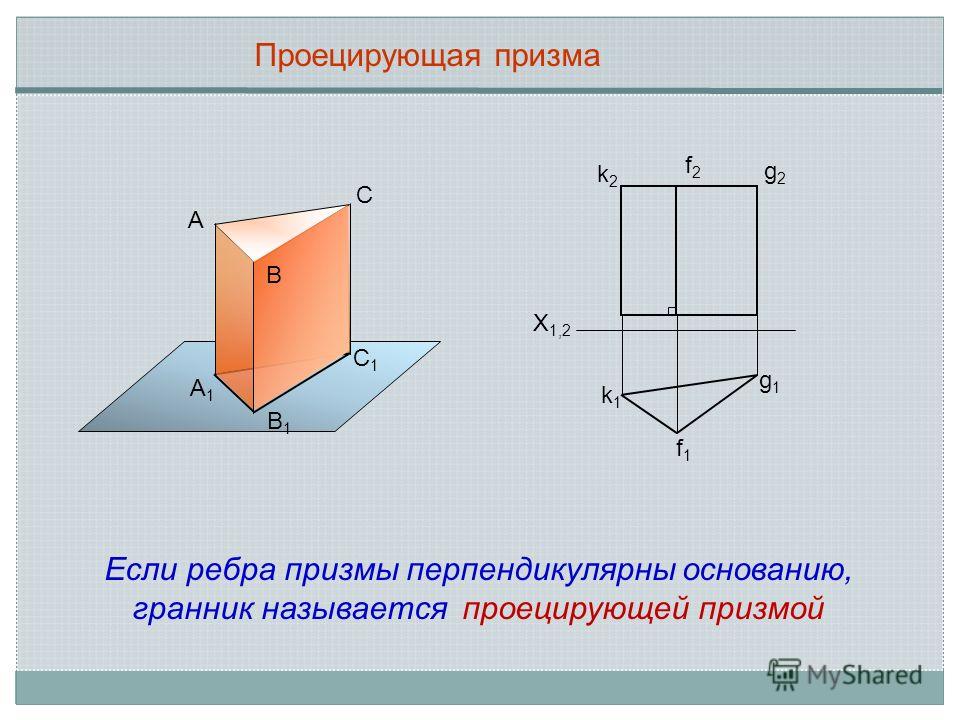
Проецирующая призма А В С С1С1 В1В1 А1А1 k2k2 k1k1 f1f1 g1g1 g2g2 f2f2 X 1,2 Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой
13
Поверхности Каталана

14
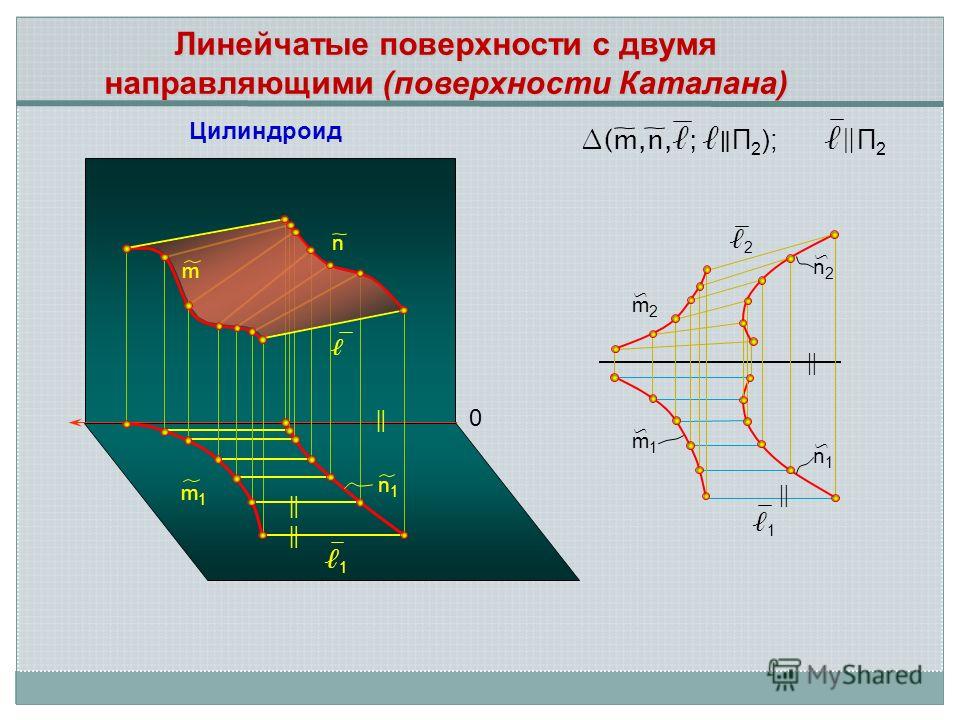
0 m1m1 n1n1 1 1 n m n1n1 m1m1 2 m2m2 n2n2 Линейчатые поверхности с двумя направляющими (поверхности Каталана) П 2 (m,n,; П 2 ); Цилиндроид
15
Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом, или косой плоскостью Гипар

16
m2m2 n2n2 n1n1 m1m1 Задача Построить каркас и очерк гипара, заданного определителем (m, n, П 2 ) I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I2 // парабола ll 1 n m ; 1 1 ll П 2 Определить видимость очерковых линий
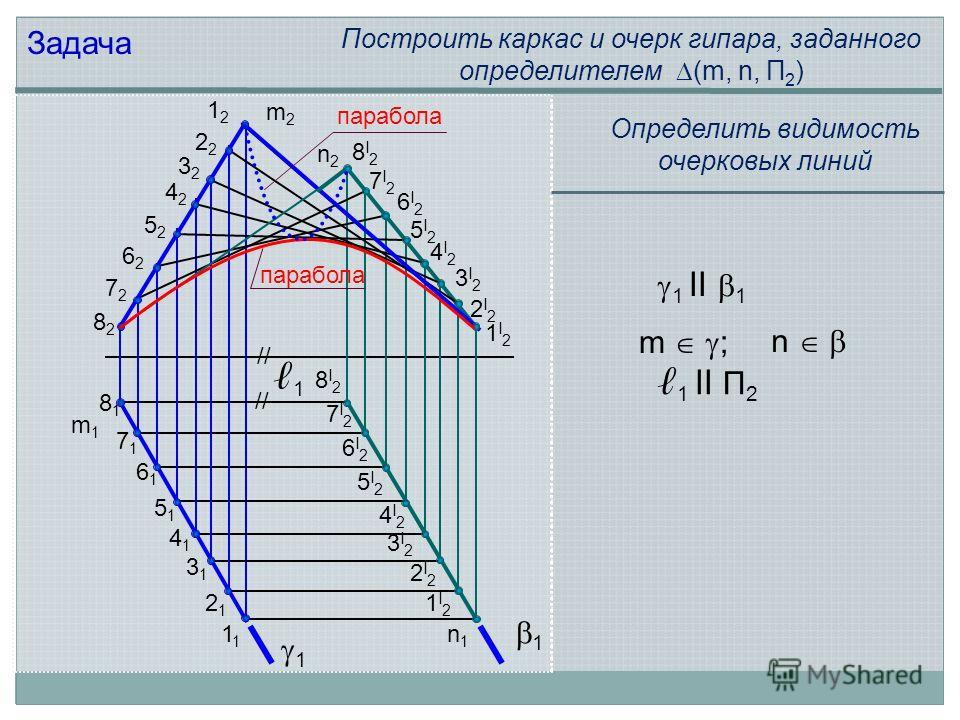
17
Винтовой поверхностью называют поверхность, образованную винтовым движением образующей Винтовым движением называют движение, при котором каждая точка А образующей вращается вокруг неподвижной оси i и одновременно перемещается поступательно вдоль этой оси Винтовая поверхность

18
n2n2 n1n1 гелиса А1А1 В1В1 ί1ί1 ί2ί2 Задача Построить каркас и очерк прямого геликоида А2А2 В2В (Прямой винтовой коноид) (n, i)
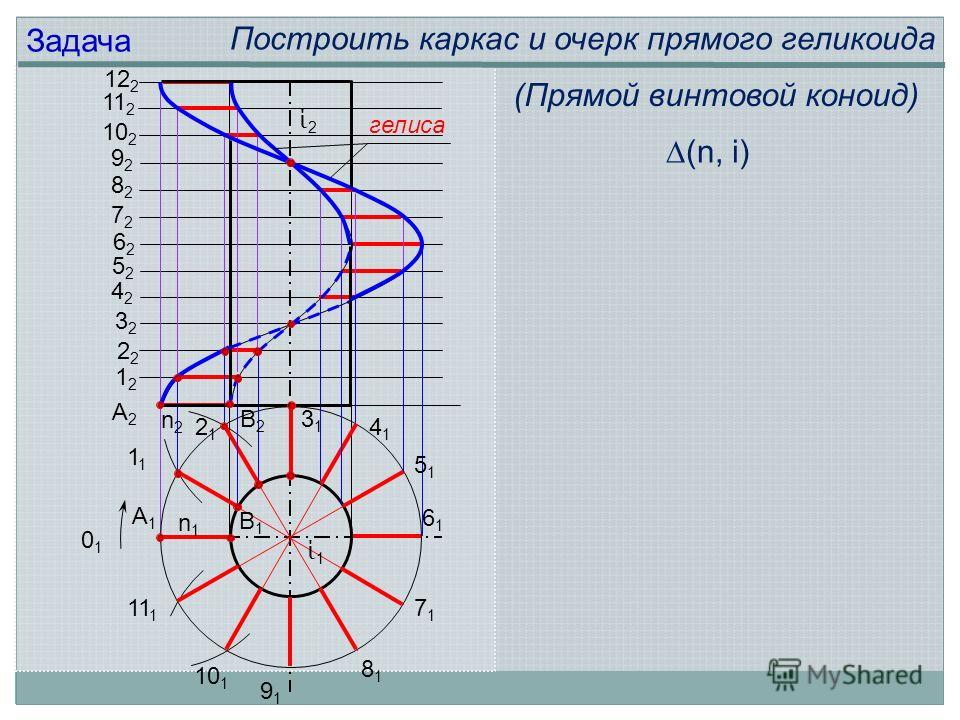
19
Задача А2А2 А1А1 В1В1 В2В2 i2i2 i1i1 Построить очерк однополостного гиперболоида вращения Однополостный гиперболоид вращения
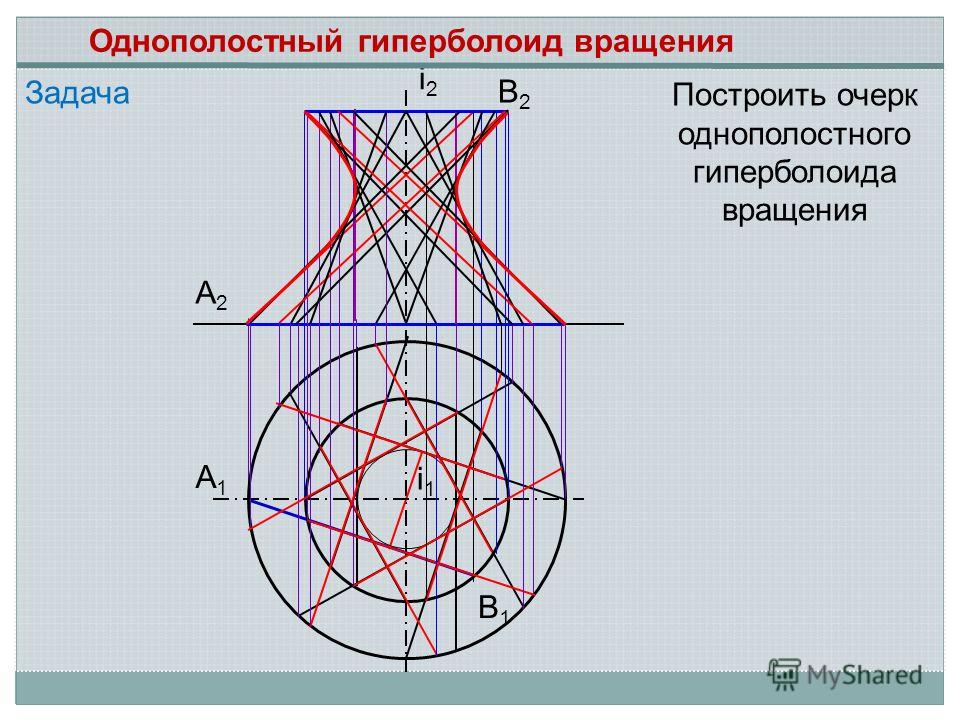
7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
 Рисунок 7.10 – Проецирование сферической поверхности
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.
 Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
Точки, линии цилиндра
Поверхности
Поверхности
Точки, линии цилиндра.
Сечение цилиндра.
Точки, линии конуса.
Сечение конуса.
Поверхности
Поверхность можно представить как общую часть нескольких смежных областей пространства.
Поверхностьесть непрерывное множество последовательных положений перемещающейся в пространстве линии. Перемещающаяся в пространстве линия называется образующей поверхности. Закон перемещения образующей называется направляющей (направляющими) поверхности. Во многих случаях образующие и направляющие взаимозаменяемы. Такой способ образования поверхности в начертательной геометрии принято называть кинематическим.
Поверхность, которая может быть образована прямолинейной образующей, называется линейчатой.Образующиминелинейчатых поверхностей являются кривые линии.
Рассмотрим определение проекции точек, расположенных на линейчатых поверхностях.
Точки, линии цилиндра
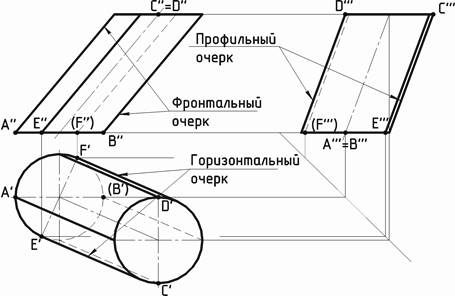
Построение проекций цилиндра сводится к построению проекций его оснований и очерковых образующих. Следует помнить, что очерковые образующие на фронтальной, горизонтальной и профильной плоскостях проекций есть разные образующие цилиндра. Так, на рисунке 1 ниже, фронтальный очерк цилиндра определяется образующими, начальные точки A и B которых находятся на нижнем основании цилиндра, и проекциями верхнего и нижнего оснований. Профильный очерк определяют образующие с начальными точками C и D на верхнем основании цилиндра и проекциями верхнего и нижнего оснований. Образующие горизонтального очерка начинаются в точках E и F на нижнем основании цилиндра. E’ и F’ – точки касания горизонтальных проекций нижнего основания цилиндра и очерковых образующих.
Очерк геометрического тела определяет границу смены видимости в проекциях.
 |
Все образующие цилиндра параллельны между собой. Поэтому для построения их проекций достаточно нахождения одной конечной точки образующей на любом основании цилиндра. Направление проекций строящихся образующих определяется направлением осевой линии цилиндра или любой очерковой образующей.
Для успешного выполнения заданий необходимо научиться анализировать положение оснований и образующих цилиндра, то есть его поверхности, относительно плоскостей проекций. Проецирующее положение образующих, а, следовательно, и поверхности цилиндра, во многом упрощает решение задачи. В этом случае одна из проекций геометрической фигуры (точки, линии, сечения), принадлежащей поверхности проецирующего цилиндра, известна, так как совпадает с той его проекцией, которая представляет собой окружность.
Точка на поверхности цилиндра может быть построена (рисунок 2):
· с помощью прямолинейной образующей (точка A);
· с помощью окружности, плоскость которой параллельна основаниям цилиндра, а центр находится на осевой линии цилиндра (точка B).
Источник
4.1 Классификация поверхностей и их изображение на чертеже
для построения проекций точек на поверхности цилиндра и конуса используются
их образующие и параллели;
положение точки на поверхности вращения определяется при помощи окружности,
проходящей через эту точку на поверхности вращения. Для построения проекций
точки поверхности вращения используются параллели;
для построения проекций точек на поверхности многогранника используются
любые вспомогательные прямые линии, принадлежащие граням.
|
|
|
|
|
|
|
Рис.65. |
-
для нахождения линии пересечения любой другой поверхности плоскостью
надо использовать вспомогательные секущие плоскости. Точки искомой линии
определяются в пересечении линий, по которым вспомогательные секущие
плоскости пересекают поверхность и плоскость;вспомогательную секущую плоскость следует выбирать так, чтобы её
линия пересечения с поверхностью проецировалась на плоскости проекций
в виде прямой или окружности; -
для построения точек пересечения прямой с поверхностью необходимо через
прямую провести вспомогательную секущую плоскость и найти линию пересечения
этой плоскости с поверхностью; точки пересечения заданной прямой и построенной
линией на поверхности и будут искомые точки пересечения прямой с поверхностью.
Пример
Определить точки пересечения прямой АВ
с поверхностью вращения.
На рис. 66
представлены горизонтальная и фронтальная проекции поверхности
вращения и прямой АВ.
Проведем через прямую АВ
фронтально проецирующую плоскость Ф
и построим линию пересечения этой плоскости с поверхностью вращения.
След плоскости Ф″
пройдет через фронтальную проекцию прямой A″
B″. Для построения линии пересечения плоскостиФ″
и поверхности вращения проведем параллели поверхности вращения
и построим горизонтальные проекции точек пересечения параллелей
с плоскостью Ф″.
Полученные точки соединим кривой линией и на пересечении горизонтальных
проекций построенной линии и прямой найдем точки Mи Nпересечения прямой АВ
с поверхностью вращения.Рис.66.
Пересечение прямой с поверхностьюЗАДАЧИ Задача 50
Лежит
ли точка А
на поверхности усеченного конуса?Задача 51
Построить
проекции линии пересечения плоскостей Ф1,Ф2,Ф3
с поверхностью цилиндра, конуса, сферы.Задача 52
Найти
точки пересечения прямойАВ
с поверхностью вращения.Задача 53
Найти
точки пересечения прямой АВ
и прямой CD
с поверхностью прямого кругового цилиндра. Построить три проекции
линии, лежащей на поверхности цилиндра. Определить видимость
проекций линии.Задача 54
Найти
точки пересечения прямой АВ
и прямой CD
с поверхностью прямого кругового конуса и построить три проекции
линии, лежащей на поверхности конуса. Определить видимость проекций
линии.Задача 55
Найти
точки пересечения прямой АВ
и прямой CD
с поверхностью сферы и построить три проекции линии, лежащей
на поверхности сферы. Определить видимость проекций линии.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь \( l \) и модуль перемещения \( s \) мяча за всё время движения?
1) \( l \)= 3,3 м, \( s \) = 3,3 м
2) \( l \) = 3,3 м, \( s \) = 0,7 м
3) \( l \)= 0,7 м, \( s \) = 0,7 м
4) \( l \)= 0,7 м, \( s \) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса \( R \). Чему равны при этом путь \( l \) и модуль перемещения \( s \) точки обода?
1)\( l=2R \), \( s=2R \)
2)\( l=\pi R \),\( s=2R \)
3)\( l=2R \),\( s=\pi R \)
4) \( l=\pi R \), \( s=\pi R \).
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
1.6. ВЗАИМНОЕ ПОЛОЖЕНИ ЛИНИИ И ПОВЕРХНОСТИ
Различают четыре возможных варианта взаимного положения линии и поверхности:
– линия и поверхность не имеют общих точек;
– линия касается поверхности;
– линия принадлежит поверхности;
– линия пересекает поверхность.
Первый вариант не рассматривают, т. к. он не имеет практического применения. Способ построения линий, принадлежащих поверхности основан на использовании ее каркаса и рассмотрен на примерах разработки комплексных чертежей поверхностей (рис. 1.54 и 1.57).
1.6.1. Построение касательной к поверхности
Задачу на построение касательной к поверхности сводят к построению касательной к линии, которая принадлежит поверхности и проходит через заданную точку.
| Из за большого объема этот материал размещен на нескольких страницах:1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Моделирование торовой поверхности
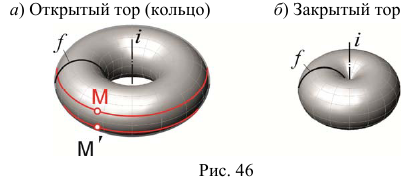
Торовая поверхность образуется вращением окружности вокруг оси, которая расположена в плоскости окружности, но не проходит через ее центр (рис. 46).
Репером торовой поверхности будут ось вращения и образующая окружность
На рис. 47 изображены три модели торовой поверхности в зависимости от взаимного положения оси вращения и образующей окружности, а также модели точек, принадлежащих контурным линиям торовой поверхности. Если ось вращения не пересекает образующую окружность то образуется открытый тор (кольцо) (см. рис. 47, а). Если же ось вращения касается образующей окружности или пересекает ее, то образуется закрытая торовая поверхность (см. рис. 47, б, в).
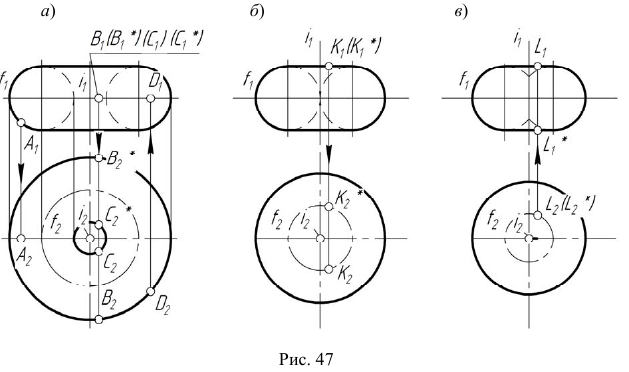

На рис. 48, а показано построение произвольной точки M, принадлежащей торовой поверхности Построение выполняется по первому алгоритму задачи 5. На рис. 48, б показано построение точки M по второму алгоритму задачи 5.
Линейчатые поверхности вращения
При вращении прямой линии, которая пересекает ось вращения в собственной или несобственной точке, образуются, соответственно, коническая или цилиндрическая поверхности. Если прямая линия скрещивается с осью вращения образуется поверхность, называемая однополостным гиперболоидом вращения.
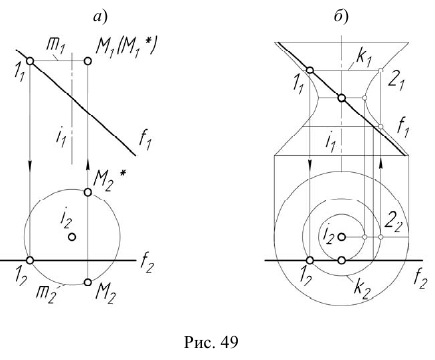
Эта поверхность также может быть получена путем вращения гиперболы вокруг ее мнимой оси. На рис. 49, а показано построение произвольной точки M, принадлежащей поверхности однополостного гиперболоида вращения а на рис. 49, б — построение фронтального очерка заданной поверхности. Через точку 1, принадлежащую образующей прямой проводится параллель поверхности вращения, после чего определяется точка 2, принадлежащая главному меридиану. Аналогично строятся все остальные точки гиперболы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пересечение прямой с плоскостью
- Пересечение прямой с поверхностью
- Пересечение поверхностей
- Способы преобразования чертежа
- Изображения и обозначения на чертежах
- Отображение пространственных объектов на плоскость
- Моделирование линии на эпюре Монжа
- Моделирование плоскости на эпюре Монжа
Касательные плоскости, развертываемые поверхности
Для необходимых здесь выводов всегда предполагается, что они также существуют.
Чтобы вычислить вектор нормали в точке, нужны частные производные представления : Икс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}
- Икстызнак равноc˙(ты)+vр˙(ты) {\ displaystyle \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} (u) + v \; \ mathbf {\ dot {r}} (u) \} ,Иксvзнак равнор(ты){\ displaystyle \ quad \ mathbf {x} _ {v} = \; \ mathbf {r} (u)}
пзнак равноИксты×Икстызнак равноc˙×р+v(р˙×р) .{\ displaystyle \ mathbf {n} = \ mathbf {x} _ {u} \ times \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} \ times \ mathbf {r} + v (\ mathbf {\ dot {r}} \ times \ mathbf {r}) \.}
Поскольку скалярное произведение (позднее произведение с двумя равными векторами всегда равно 0!), В каждой точке есть касательный вектор . Касательные плоскости вдоль этой прямой идентичны, если они кратны . Это возможно только в том случае, если три вектора лежат в одной плоскости, т.е. ЧАС. линейно зависимы. Линейную зависимость трех векторов можно определить с помощью определителя этих векторов: п⋅рзнак равно{\ Displaystyle \ mathbf {п} \ cdot \ mathbf {r} = 0}р(ты){\ Displaystyle \ mathbf {r} (и_ {0})}Икс(ты,v){\ Displaystyle \ mathbf {х} (и_ {0}, v)}р˙×р{\ displaystyle \ mathbf {\ dot {r}} \ times \ mathbf {r}}c˙×р{\ displaystyle \ mathbf {\ dot {c}} \ times \ mathbf {r}}c˙,р˙,р {\ Displaystyle \ mathbf {\ точка {с}} \ ;, \; \ mathbf {\ точка {r}} \ ;, \; \ mathbf {r} \}
Касательные плоскости вдоль прямой совпадают, еслиИкс(ты0,v)знак равноc(ты0)+vр(ты0){\ displaystyle \ mathbf {x} (u_ {0}, v) = \ mathbf {c} (u_ {0}) + v \; \ mathbf {r} (u_ {0})}
-
- Det(c˙(ты),р˙(ты),р(ты))знак равно .{\ displaystyle \ det (\ mathbf {\ dot {c}} (u_ {0}) \ ;, \; \ mathbf {\ dot {r}} (u_ {0}) \ ;, \; \ mathbf {r } (u_ {0})) \; = \; 0 \.}
- Генеративная форма, к которой это применимо, называется торсальной .
Линейчатая поверхность точно тогда раскручивается в плоскость, когда для всех точек гауссова кривизна равна нулю. Это так тогда и только тогда, когдаИкс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}
-
-
- Det(c˙,р˙,р)знак равно{\ displaystyle \ det (\ mathbf {\ dot {c}} \; \; \ mathbf {\ dot {r}} \ ;, \; \ mathbf {r}) \; = \; 0 \ quad}
-
- применяется в каждой точке, d. т. е. если каждый образующий – торсальный. Поэтому развивающуюся область также называют торсом .
Свойства развертывающейся поверхности:
- Генераторы представляют собой семейство асимптотических линий , а также семейство линий кривизны .
- Разворачивающаяся поверхность – это либо (общий) цилиндр, либо (общий) конус, либо касательная поверхность (поверхность, состоящая из касательных пространственной кривой).


































