Пружинный маятник: амплитуда колебаний, период, формула

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию

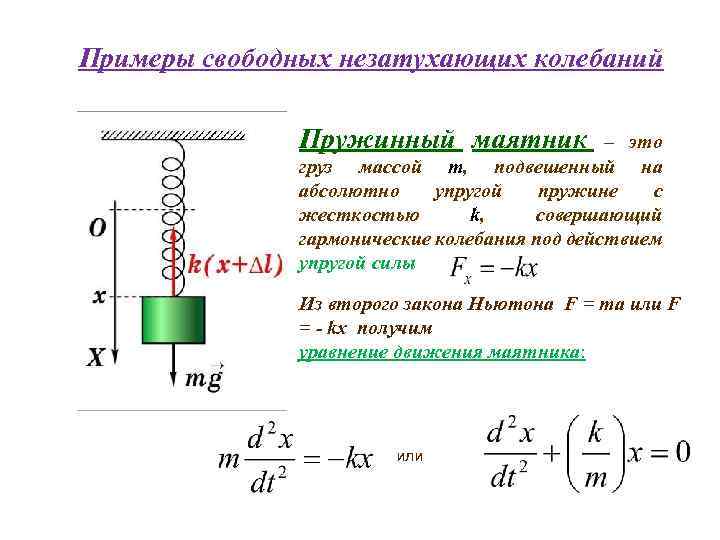
Цель урока: рассмотреть процесс колебаний на примере нитяного и пружинного маятников, выяснить зависимость периода колебаний от различных физический величин: длины нити, ускорения свободного падения, коэффициента жесткости и массы.

1. Проверка домашнего задания. (работа по формуле “Скажи ты. )

— Что называется амплитудой колебания; периодом колебания; частотой колебания; циклической частотой?

— Какой буквой обозначается циклическая частота?

— Какая математическая зависимость существует между периодом и частотой колебания?

Учащиеся в парах проверяют домашнюю работу: упражнение №24.

2. Объяснение нового материала. Работа по теме урока.

Учитель. Как вы думаете, от каких величин может завесить период колебаний нитяного маятника?

Ученики. От длины нити и массы груза.

Учитель. Начнем с длины нити. Поставим опыт с двумя маятниками, имеющими разную длину нити, но одинаковую массу (эксперимент).

Ученики. С увеличением длины нити период колебаний увеличивается.

Учитель. А теперь посмотрим как зависит период колебаний от массы груза (эксперимент: маятники имеют одинаковую длину нити и разный вес грузов).

Учащиеся. Период не зависит от массы груза.

Учитель. Но период колебания нитяного маятника зависит еще от одной физической величины. Это ускорение свободного падения. Проведем эксперимент и “поможем “ силе тяжести положив магнит. Теперь при той же массе груза возвращающая сила будет больше.

Ученики. Период уменьшился, а частота увеличилась.

Учитель. А теперь выведем формулу для расчета периода колебания нитяного маятника.

формула Гюйгенса:

g – ускорение свободного падения.

Это очень важная формула и ее надо запомнить.

Учитель. От чего может зависеть период пружинного маятника?

Ученики. От жесткости пружины, массы груза.

Учитель. Сначала на опыте посмотрим зависимость периода колебаний и жесткости пружины.(эксперимент : две пружины разной жесткости, но одинаковой длины и одинаковой массой груза)

Ученики. Период меньше там, где жесткость больше.

Учитель. А как вы думаете как зависит период от массы груза(эксперимент).

Ученики. Чем больше масса , тем больше и период.

Учитель. А теперь выведем формулу для расчета периода колебания пружинного маятника.

— возвращающая сила системы

— собственная частота системы.

Эту формулу так же запишите на обложку тетради и постарайтесь ее запомнить.

3. Закрепление материала

Решение задач Лукашик В.И.№ 873, 876.879

4.Домашнее задание. Лукашик В.И.№ 875, 877.880.

Список литературы:

1.Л.Э.Генденштейн,В.А.Орлов,Г.Г.Никифоров “Как научить решать задачи по физике (основная школа ). Подготовка к ГИА.

2. С.Е.Полянский “Поурочные разработки по физике”.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Формула для расчета периода колебаний пружинного маятника

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке! Жмите СЮДА

Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается

Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.

Давайте выведем формулу периода пружинного маятника.

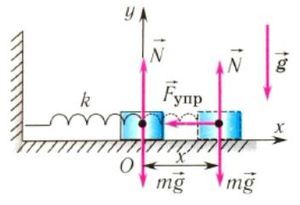
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :

Все проецируем на ось ОХ:

Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:

Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

Тогда период колебаний пружинного маятника будет равен:

• Период физического маятника
• Период крутильного маятника
• В Формуле мы использовали :
• — Период пружинного маятника маятника
• — Масса груза
• — Изменение длины пружины
• — Коэффициент упругости пружины
• — Ускорение свободного падения
• — Циклическая частота пружинного маятника
• — Сила реакции опоры
• — Сила упругости

Формула периода колебаний пружинного маятника

1. Период — это минимальное время, за которое совершается одно полное колебательное движение.
2. Обозначают период буквой $T$.
3. где $Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1).

Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести.

Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

• Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
• Ускорение груза запишем, помня, что движение происходит по оси X, как:
• Второй закон Ньютона для груза принимает вид:
• Учтем равенство (2), формулу (5) преобразуем к виду:
• Если ввести обозначение: $^2_0=frac$, то уравнение колебаний запишем как:
• где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
• где $_0=sqrt>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

смещение положения равновесия точки

смещение положения равновесия точки

Задача 40713

Написать уравнение синусоидального гармонического колебания, если амплитуда скорости 63 см/с, период колебаний 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найти амплитуду ускорения, частоту колебаний.

Задача 40738

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 см/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 25 мм. Найти амплитуду скорости.

Задача 40739

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 м/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 0,25 мм. Найти амплитуду скорости.

Задача 26216

Написать уравнение гармонических колебаний с амплитудой 50мм, периодом 4с и начальной фазой П/4. Найти смещение точки от положения равновесия при t = 0 и t = 1,5 с.

Задача 26560

Уравнение незатухающих колебаний дано в виде: У = 4 ·10–2cos6πt, м. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний через 0,01 с после начала колебаний. Скорость распространения колебаний 340 м/с.

Задача 11103

Напишите уравнение гармонического колебания, если амплитуда скорости vm = 63 см/с, период колебаний Т = 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найдите амплитуду ускорения и частоту колебаний. Постройте график зависимости смещения от времени.

Задача 12666

На каком ближайшем расстоянии от источника колебаний с периодом 45 мс через время, равное половине периода после включения источника смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний равна 158 м/с. Считать, что в момент включения источника все точки находятся в положении равновесия.

Задача 14576

Уравнение незатухающих колебаний х = 4sin(600πt) см. Найти смещение x от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01с после начала колебаний. Скорость распространения колебаний v = 300 м/с.

Задача 14932

Плоская монохроматическая волна распространяется вдоль оси Y. Амплитуда волны А = 0,05 м. Считая, что в начальный момент времени смещение точки Р, находящейся в источнике, максимально, определить смещение от положения равновесия точки М, находящейся на расстоянии у = λ/2 от источника колебаний в момент времени t = T/6.

Задача 15330

Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний, в момент времени Т/6 равно половине амплитуды. Найти длину бегущей волны.

Задача 17372

Начальная фаза гармонического колебания ψ = 0. При смещении точки от положения равновесия х1 = 2,4 см скорость точки v1 = 3 см/с, а при смещении х2 = 2,8 см ее скорость v2 = 2 см/с. Найти амплитуду А и период Т этого колебания.

Задача 19324

На каком расстоянии от источника колебаний, совершаемых по закону синуса, в момент времени t = T/2 смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний 340 м/с. Период колебаний 10–3 с.

Задача 19326

Источник плоских волн совершает колебания по закону x = A cos ωt. Через четверть периода после начала колебаний смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника, равно половине амплитуды. Найти длину бегущей волны.

Задача 19327

Источник плоских волн совершает колебания по закону x = A cos ωt. Какова амплитуда колебаний, если смещение от положения равновесия точки, отстоящей от источника на расстоянии λ/12 для момента времени T/4, равно 0,025 м?

Задача 20380

Определить начальную фазу колебаний, которые происходят по закону косинуса, если максимальная скорость равна 16 см/с, период колебаний 1,4 с, а смещение точки от положения равновесия в начальный момент времени составляет 2,84 см.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Основные виды полуосей

Зависимо от конструкции полуось может быть полностью или частично разгруженной от действующих на нее изгибающих моментов.

Разгруженная полуось

более характерна для транспортных средств с большой грузоподъемностью, в том числе автобусов. Такая полуось на чертеже будет выглядеть свободно установленной внутри моста деталью, а опираться на балку моста будет ступица колеса с помощью двух подшипников. В данной конструкции полуось передает исключительно крутящий момент, поскольку всю силу изгибающего воздействия на себя принимают подшипники.

Виды полуосей

Полузагруженная полуось

в подавляющем большинстве случаев установлена на легковых и легкогрузовых автомобилях. Устройство полуоси данного вида отличается тем, что в ней подшипник стоит между самой полуосью и ее кожухом, причем полуось крепится непосредственно к ступице колеса. По этой причине на плече периодически возникают изгибающие моменты, которые воздействуют на полуоси в вертикальной и горизонтальной плоскостях.

На переднеприводных автомобилях для передачи крутного момента от КПП к колесам устанавливаются полуоси несколько иной конструкции. Состоит такой приводной вал из оси, внутреннего и наружного ШРУСов.

Устройство приводного вала переднеприводного автомобиля.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

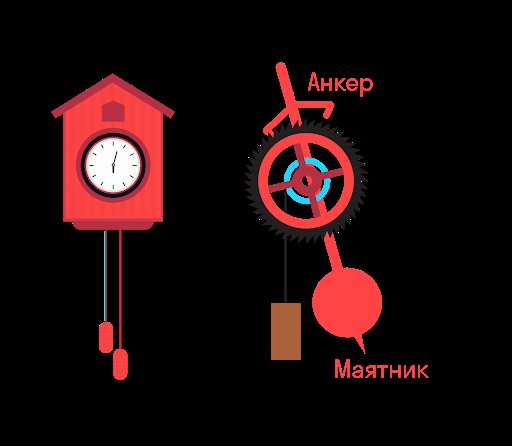
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Механика приводов. Редукторы. Передаточные механизмы. Характеристики типовых упругих элементов

Лекция 1

Механика приводов

В приводе любой технологической машины имеются механические устройства, преобразующие движение выходного элемента приводного двигателя (вращательное или поступательное) в движение её исполнительного органа. Эти устройства образуют кинематические схемы машин, конкретные исполнения которых

бесконечно многообразны. Они состоят из большого

Рис.1

a- редуктор, б – зубчато-реечная передача, в – шатунно-кривошипный механизм, г –грузоподъемное устройство, д- передача винт-гайка, е – передача винт-гайка качения.(шарико-винтовая передача – ШВП)

количества различных элементов, таких как соединительные муфты, валы и оси, редукторы, рычажные механизмы, передаточные устройства, преобразующие вращательное движение в поступательное и наоборот. Примеры таких устройств показаны на рис. 1.

Статические и динамические характеристики механической системы привода оказывают существенное влияние на работу технологической машины и, в частности, на работу ее приводов. Рассмотрим некоторые параметры элементов кинематических схем, отражающие их основные свойства.

Редукторы

(рис.1-а) различных типов изменяет угловую скорость при передаче движения с на . Каждый элемент редуктора характеризуется своей угловой скоростью , ,…, а также передаточным отношением отдельных ступеней передачи, например,

, (1)

где и соответственно угловые скорости ведущего и ведомого валов.

Передаточные механизмы,например, зубчато-реечная передача (рис.1-б),грузоподъёмное устройство (рис. 1- г),передачи винт гайка и винт – гайкакачения (рис.1 д и е) преобразует вращательное движение шестерни с угловой скоростью в поступательное движение рейки с линейной скоростью V. При этом передаточное отношение

(2)

называют радиусом приведения линейной скорости V к валу со скоростью вращения . В отличие от передаточного отношения редуктора (коэффициента редукции) передаточное отношение имеет размерность .

Шатунно-кривошипный механизм

(рис. 1-в) преобразует вращательное движение кривошипа с постоянной скоростью в возвратно-поступательное движение ползуна с переменной линейной скоростью V(t).

Характеристики типовых упругих элементов.

При нагружении многие элементы кинематических цепей подвергаются упругим деформациям, в результате чего механическая часть привода не может всегда рассматриваться как абсолютно жесткое тело. В кинематических цепях наиболее податливыми являются элементы передаточных устройств, характеристики которых рассматриваются ниже. Однако полученные характеристики могут быть использованы и для других устройств кинематических цепей.

Вал, работающий на кручение

(рис.2-а), характеризуется углом закручивания

, (3)

где М — приложенный к валу вращающий момент, — длина вала, G – модуль упругости второго рода, — полярный момент инерции сечения вала.

Коэффициент жесткости определяется отношением

, êï. (4)

Растягиваемый или сжимаемый стержень

(рис.2-б) к которому приложена сила F, имеет следующее значение жесткости (ньютон на метр)

, ïê (5)

где — линейная деформация стержня, — Модуль упругости первого рода, S – площадь стержня.

Цилиндрическая зубчатая передача.

При закрепленной ступице ведущего колеса 1 приложим момент к колесу 2 (рис.2 -в). Вследствие деформации зубьев колесо 2 повернется на угол . Таким образом, жесткость передачи может быть определена по формуле (4). Однако в этом случае жесткость следует считать приведенной к оси колеса 2 ( можно и к оси колеса 1). Таким образом

. (6)

Так как

то . (7)

Итак, жесткость, приведенная к оси ведомого колеса 2, в раз больше жесткости, приведенной к оси ведущего колеса 1.

Ременные и цепные передачи

(рис.2-г). Если жесткость ремня или цепи на растяжение, то при повороте ведомого звена 2 на угол и закрепленном ведущем звене 1 в натянутой ветви возникает сила где — радиус ведомого звена.

Отсюда находим: , (8)

где — жесткость, приведенная к оси ведомого звена; — коэффициент вида передачи. Для ременной передачи для цепной передачи

По формуле (8) можно определить жесткость канатов в барабанных передачах грузоподъемных устройств, канатных дорог и других подобных устройств, где принимают

Соединительные муфты

являются неотъемлемой частью всех передаточных устройств. Они делятся не жесткие, полужесткие и упругие. С помощью муфт осуществляется не только механическое соединение